WSRC-TR-2000-00161
Bubble Formation Modeling in IE-911
F. F. Fondeur, D. D. Walker, W. R. Wilmarth,
and S. D. Fink
Westinghouse Savannah River Company
Aiken, SC 29808
This report was prepared as an account of work sponsored by an agency of the United States Government. Neither the United States Government nor any agency thereof, nor any of their employees, makes any warranty, express or implied, or assumes any legal liability or responsibility for the accuracy, completeness, or usefulness of any information, apparatus, product or process disclosed, or represents that its use would not infringe privately owned rights. Reference herein to any specific commercial product, process or service by trade name, trademark, manufacturer, or otherwise does not necessarily constitute or imply its endorsement, recommendation, or favoring by the United States Government or any agency thereof. The views and opinions of authors expressed herein do not necessarily state or reflect those of the United States Government or any agency thereof.
This report has been reproduced directly from the best available copy.
Available for sale to the public, in paper, from: U.S. Department of Commerce, National Technical Information Service, 5285 Port Royal Road, Springfield, VA 22161, phone: (800) 553-6847, fax: (703) 605-6900, email: orders@ntis.fedworld.gov online ordering: http://www.ntis.gov/support/ordering.htm
Available electronically at http://www.osti.gov/bridge/
Available for a processing fee to U.S. Department of Energy and its contractors, in paper, from: U.S. Department of Energy, Office of Scientific and Technical Information, P.O. Box 62, Oak Ridge, TN 37831-0062, phone: (865 ) 576-8401, fax: (865) 576-5728, email: reports@adonis.osti.gov
Summary
The author used diffusion modeling to determine the hydrogen and oxygen concentration inside IE-911. The study revealed gas bubble nucleation will not occur in the bulk solution inside the pore or on the pore wall. This finding results from the fast oxygen and hydrogen gas molecular diffusion and a very confined pore space. The net steady state concentration of these species inside the pore proves too low to drive bubble nucleation. However, gas bubbles can form at defects (i.e., missing IE-910 particles or excessive binder or voids) inside the IE-911 or open spaces larger than 300 Å. This study did not investigate other gas bubble nucleating mechanism such as suspended particles in solution.
Keywords: waste processing, hydrogen, oxygen, bubble nucleation
Introduction
The Savannah River Site (SRS) continues to examine three processes for the removal of cesium from high-level waste. One option involves the use of crystalline silicotitanate (CST) as a non-elutable ion exchange medium. The process involves adding CST in its engineered form – IONSIVTM IE-911 made by UOP, LLC. – to a column and passing the liquid waste through the column. Cesium exchanges with sodium ions residing inside the CST particles. The design disposes of the cesium-loaded CST by vitrification within the Defense Waste Processing Facility.
Work to date has defined several technical risks for the CST technology.1 Cesium-loaded CST will remain in the column for several months. During this period, radiation-induced gas generation will occur in the liquid. Gas bubble formation inside the pores of the CST could, in principle, hinder transportation or completely exclude volume fractions of the pore from liquid contact. Before gas bubbles can form, soluble gas molecules must congregate and nucleate. Nucleation occurs at a certain level of supersaturation based upon the presence of nucleation sites; gas generation and diffusion are opposing factors in determining concentration. The factors governing gas accumulation (or concentration) include the G-value (i.e., amount of gas molecules generated by radiolysis per 100 eV of deposited energy), gas molecule adsorption on the pore walls, gas molecule diffusion rate, and mass transfer rate out of the pore ends (film transfer theory).2 Of these factors, generation due to radiation and diffusion significantly affect gas concentration in the pore.
The current work investigates the net gas molecule accumulation inside the pore. The calculated hydrogen and oxygen concentrations are inserted into the Young-Laplace equation to determine if gas bubbles form as a result.
Gas Molecule Accumulation Inside the Pore
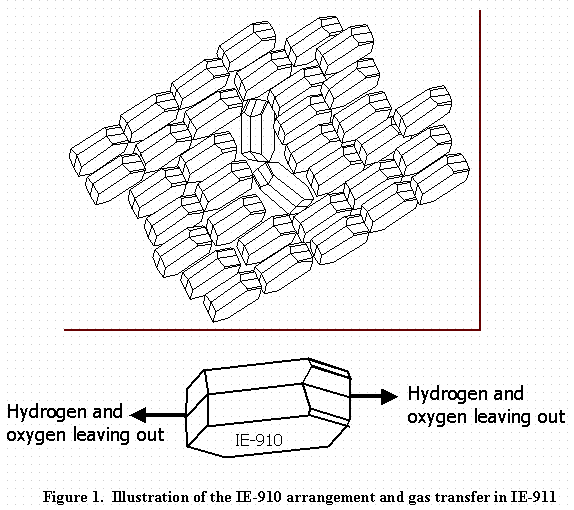
The particle size of IE-911 ranges from 500 to 600 mm in diameter. The particle contains an agglomeration of IE-910 (0.2 · M diameter) particles stuck together with a binder material (see Figure 1 for a small portion of IE-911). For simplicity, the authors assume a single continuous pore with tortuosity equal to reported values of IE-911.3 The investigation looked at two situations. The calculations assumed that at the ends of the pore, either gas-molecule flux in or out of the pore remains constant, or gas concentration remains constant. In either case, the gas molecule concentration inside the pores derives from the following mass balance equation.

The calculations assumed that, at the ends of the pore, either gas-molecule flux in or out of the pore remains constant or gas concentration remains constant. In either case, the gas molecule concentration inside the pores derives from the following mass balance equation.

In this equation we adjust diffusivity for tortuosity (t =35) and pore confinement (by definition D= Dbulk x pore confinement (=0.7)/ tortuosity). Under the condition of constant flux at the pore exit, application of Fourier Transform techniques yields the following general solution.4
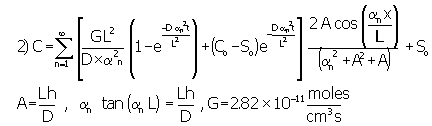
Assuming the length of the pore "L" as 600 mm
(as determine from SEM images), Table 1 lists the steady-state hydrogen and
oxygen concentrations.
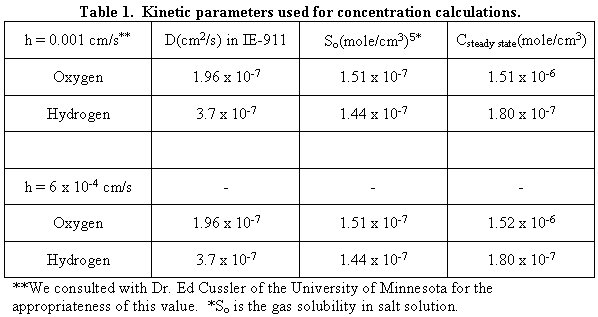
In Table 1, the symbol "h" stands for film transfer coefficient or the rate at which oxygen or hydrogen exits the pore. The symbol "D" stands for oxygen or hydrogen diffusivity. The oxygen diffusivity in water equals 2.41 x 10-5 cm2/s.6 We corrected the diffusivity for SRS solution through the Einstein-Stoke relationship as shown below.
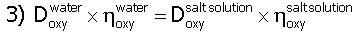
Dwater is 2.41 x 10-5, h water is 10-3 kg /m*s and h Salt Solution is 2.64 x 10-3 kg/ms.7 We then adjusted the corrected oxygen diffusivity for tortuosity (t = 35) and pore confinement (0.7) in IE-911.8 Pore confinement was based on a pore radius of 20 x 10-8cm. This is the maximum gas bubble radius in the pore (B.E.T. nitrogen chemisorption test showed a very narrowed, 20 ± 0.7 Å radius) and the bigger the gas bubble the easier it can nucleate. Therefore, we chose a gas bubble radius of 20 x 10-8 cm for all the calculations. We obtained the hydrogen diffusivity from the oxygen diffusivity through the Wilke and Chang relationship9 as shown below.

In this equation "VI" is the molar volume of the i-species. The hydrogen diffusivity in SRS salt solution obtained by this method is 1.85 x 10-5 cm2/sec. When this value is substitute in Eq. 3, the hydrogen diffusivity in a diluted solution of pure water obtained is 4.88 x 10-5 cm2/sec. This is very close to the literature value of 4.8 x 10-5 cm2/sec.10 In Table 1, both oxygen and hydrogen concentrations are independent of the film transfer coefficients used in this study. The calculations gave expected concentration profiles along the pore length as shown in Figures 2 and 3.
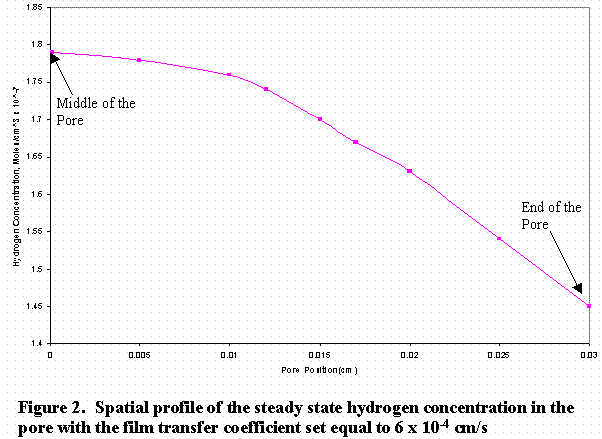
In Figure 2, the zero-position on the abscissa of the graph represents the middle of the pore and the 0.03 point represents the exit. Figure 3 shows the temporal evolution of the concentration with time at the middle of the pore.
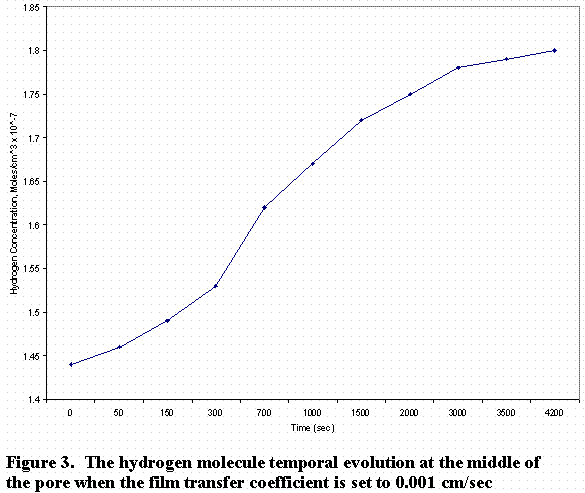
As can be seen from Fig. 3, the concentration at the middle reaches steady state after 1.5 hours. When the oxygen or hydrogen concentration remains constant (i.e., equal to the saturation concentration) at the pore exit, one can calculate the concentration from equation 4.
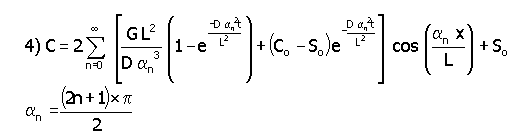
In this equation, the eigenvalues (an) do not depend on the film transfer coefficient, diffusivity, or IE-911 radius. Substituting for the kinetic variables used for the previous case, the steady state [O2] at the center of the pore equals 1.91 x 10-6 moles/cm3 and [H2] equals 1.08 x 10-6 moles/cm3. Since these values are higher than those reported in Table 1, we chose these values for the formation of gas bubble in IE-910. Note [O2] is higher than the [H2] because of its lower diffusivity.
Gas Bubble Formation Criteria
Mechanical Equilibrium Condition for Homogeneous Nucleation
Gas bubbles can form in the bulk liquid of the pore (homogeneous) or on the surface of the pore (heterogeneous). In the former case, the excess pressure from hydrogen and oxygen molecules must overcome the hydrostatic and surface tension pressure, as indicated in equation 5 (Young-Laplace equation), before a bubble form.
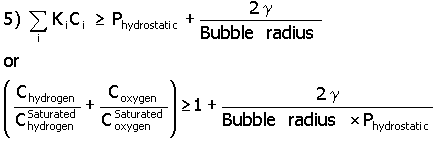
In this equation Ki is the Henry’s Law gas constant for hydrogen and oxygen. For a KH value of 7.03 x 109 kg cm2/s2mole*, a KO value of 6.71x 109 kg cm2/s2 mole, a g (surface tension) value of 0.03 kg/s2,11 a gas bubble radius of 20 x 10-8 cm (the pore radius of IE-910) and using the concentration values of Table 1, one determines that a gas bubble can not form as shown in equation 6.
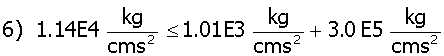
As can be seen in equation 6, mechanical equilibrium shows no bubble can form in the bulk liquid phase inside the pore (in IE-910 pore size). Atmospheric pressure is set at 1013.25 Kg/cm*s2.
Mechanical Criteria for Heterogeneous Nucleation on the Pore Walls
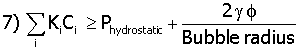
where f is a trigonometry function dependent on the wetting angle between liquid phase in the pore and the IE-910. The value of f comes from equation 8.12
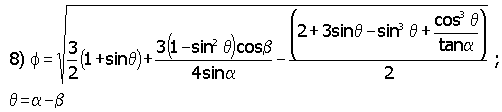
In this equation, b is the wetting angle between the liquid phase and the solid IE-910. The quantity a is an angle describing the opening of a defect and q is a difference angle between a and b as illustrated in Figure 4.
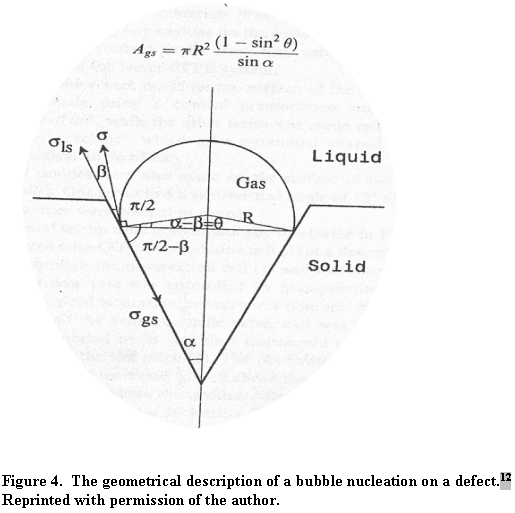
When surfaces exist for gas nucleation, the supersaturation required for nucleation varies with wetting angle between the liquid phase and solid surface. When the liquid readily wets the surface (b < 30°), large supersaturation proves necessary for bubble nucleation. The value of f is different from 0 and may be larger than 1. That is, in small-bore defects (a » 0), supersaturation of the order shown in equation 5 is required. Stated in another way, no gas will form or remain trapped in sharp notch cracks (i.e., small opening cracks in the pores). When the liquid does not wet the solid (i.e., b = 180 or greater) no supersaturation or, depending on the defect opening, sub-saturation can produce bubbles. Figure 5 best illustrates this phenomenon.
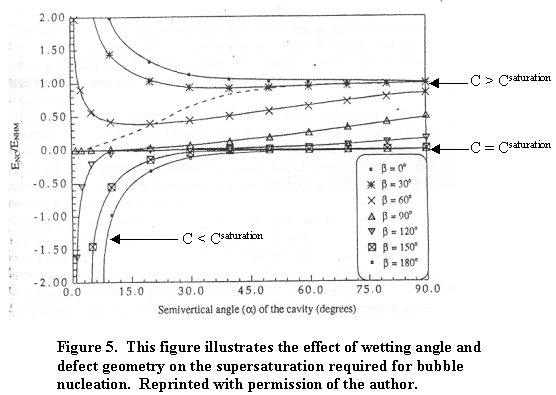
Private communication with UOP, LLC, revealed SRS salt solutions should readily wet IE-911.13 This implies a small wetting angle (b < 30°). Therefore, supersaturation of the order shown in equation 7 will result in bubble formation. Assuming IE-910 as a crystalline defect-free zeolite (a is near 180°), supersaturation comes from equation 10.12 Substituting b = 30° and the KH, KO and the concentrations listed in Table 1 into Equation 9 predicts that a bubble will not form on the pore wall. However, bubbles will form in the void areas of the IE-911 (missing IE-910) whether filled with binder or not. This is because the binder has pore sizes in the range of 0.1 mm where this equation predicts bubble formation.
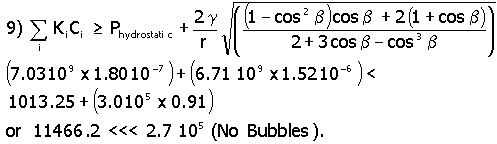
Conclusion
Diffusion modeling of hydrogen and oxygen concentration inside IE-911 revealed gas bubble nucleation will not occur in the bulk solution inside the pore or on the pore wall. This finding results from the fast oxygen and hydrogen gas atom diffusion. The net steady state concentration of these species inside the pore proves too low to drive bubble nucleation. However, gas bubbles can form at defects inside the IE-911 because the voids with diameter 300 Å or higher surface tension do not contribute significantly. This study did not consider other nucleating mechanism such as particle suspension (colloidal solutions).
References