G. J. Hutchens and N. K. Gupta
Westinghouse Savannah River Company
Aiken, SC 29808

This report was prepared as an account of work sponsored by an agency of the United States Government. Neither the United States Government nor any agency thereof, nor any of their employees, makes any warranty, express or implied, or assumes any legal liability or responsibility for the accuracy, completeness, or usefulness of any information, apparatus, product or process disclosed, or represents that its use would not infringe privately owned rights. Reference herein to any specific commercial product, process or service by trade name, trademark, manufacturer, or otherwise does not necessarily constitute or imply its endorsement, recommendation, or favoring by the United States Government or any agency thereof. The views and opinions of authors expressed herein do not necessarily state or reflect those of the United States Government or any agency thereof.

This report has been reproduced directly from the best available copy.

Available for sale to the public, in paper, from:  U.S. Department of Commerce, National Technical Information Service, 5285 Port Royal Road, Springfield, VA 22161,  phone: (800) 553-6847,  fax: (703) 605-6900,  email:  orders@ntis.fedworld.gov   online ordering:  http://www.ntis.gov/support/ordering.htm

Available electronically at  http://www.osti.gov/bridge/

Available for a processing fee to U.S. Department of Energy and its contractors, in paper, from: U.S. Department of Energy, Office of Scientific and Technical Information, P.O. Box 62, Oak Ridge, TN 37831-0062,  phone: (865 ) 576-8401,  fax: (865) 576-5728,  email:  reports@adonis.osti.gov

A desktop program is developed in Microsoft EXCEL using Visual Basic for Applications (VBA) to solve a two-dimensional steady state heat conduction problem with a radiation boundary condition. The resulting partial differential equation and boundary conditions are solved using finite difference techniques and the results are compared with a finite element solution using the commercially available software package MSC/THERMAL. The results from the two methods are found to be within 1%. The VBA solution demonstrates how spreadsheet programs, like EXCEL, can be used to solve practical engineering problems with good accuracy.

Keywords: thermal radiation, Gauss-Seidel iteration, concrete temperature, spreadsheet

In the last decade, spreadsheet programs such as Microsoft EXCEL have advanced far beyond their original financial and office environment applications. Today, spreadsheets are a common tool used in engineering analyses, including the numerical solution of engineering boundary value problems. [1-3] The objective here is to use an EXCEL spreadsheet to analyze an engineering problem of practical interest, namely, to estimate the two-dimensional steady-sate temperature distribution in a concrete wall subject to thermal radiation on one of its boundaries. The analysis will include the numerical solution of the nonlinear heat conduction problem associated with determining the temperature distribution in the wall.

Prior to version 5, EXCEL used a macro language called XLM. [4] With XLM it was possible to group together functions (XLM commands) to form rudimentary programs. These programs could then be used in various applications. However, beginning with version 5, EXCEL introduced Visual Basic for Applications (VBA) as the macro language that offers several advantages over XLM, including ease of maintenance as well as easier to understand code.

The paper begins by presenting the model equations and boundary conditions giving the steady-state temperature distribution. Then, the finite difference approximations of the model equations are derived and the solution algorithm is described. Finally, the results of the analysis are presented and discussed. The results are also compared with a general purpose thermal conduction/radiation code (MSC/THERMAL).

Consider a two-dimensional region of height a, (associated with the x-coordinate) and width b (associated with the y-coordinate). With no internal heat generation, the steady-state temperature distribution, T(x, y), is given by

where T is given in ^oC, the coordinate x ranges from zero to a (in m), and the coordinate y ranges from zero to b (in m). Since no heat is generated internal to the region, energy flow is determined by prescribed temperatures or heat fluxes on the boundary surfaces.

It is assumed that the surface at x = 0 is heated by thermal radiation at temperature T_s (in ^oC), the surface at x = a is at the constant temperature T_gr (in ^oC), the surface at y = 0 is cooled by natural convection to a gas at temperature T_air (in ^oC), and the surface at y = b is cooled by natural convection at temperature T_cell (in ^oC). Now the boundary conditions for Eq. (1) may be written as

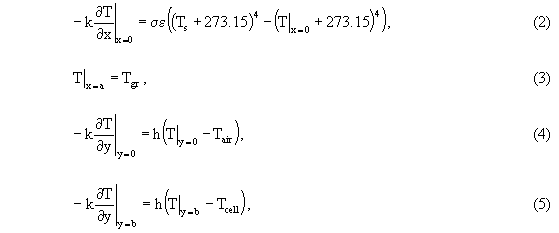
where s is the Stefan-Boltzmann constant, e is the emissivity of the surface at x = 0, k is the thermal conductivity (assumed constant), the factor 273.15 is the conversion from ^oC to K, and h is the heat transfer coefficient due to natural convection (assumed constant).

With the inclusion of thermal radiation, the heat conduction problem defined by Eqs. (1) through (5) is nonlinear, which makes it difficult to solve since the superposition of solutions is no longer valid. An approximate analytical solution may be constructed by first linearizing the radiation boundary condition, Eq. (2). Then, classical methods for solving partial differential equations, such as integral transforms, may be used. [5] On the other hand, the nonlinear heat conduction problem may be solved numerically using Gauss-Seidel iteration or Newton's method. [6, 7] Note that by solving the problem numerically, the radiation boundary condition may be treated directly.

To solve the finite difference approximation of Eqs. (1) through (5) using Newton's method requires the construction of the Jacobian matrix associated with the resulting set of algebraic equations. However, numerically evaluating the partial derivatives in the Jacobian matrix can be time-consuming and lead to a loss of precision. As an alternate approach, since the nonlinearity is in the radiation boundary condition and not the heat conduction equation itself, the finite difference approximation of Eqs. (1) through (5) may be easily solved using Gauss-Seidel iteration.

To derive the finite difference approximation of Eqs. (1) through (5), first, associate the index "j" with the x-coordinate and the index "k" with the y-coordinate so that the temperature, T(x, y), becomes T_j,k. Then, average Eqs. (1) through (5) over a finite difference zone of "volume" D xD y (where it is assumed that D x and D y are constant but not necessarily equal). With this, Eq. (1) becomes

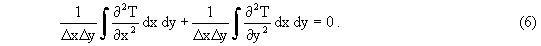
Carrying through the integration gives the finite difference approximation for Eq. (1), namely,

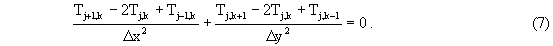
Likewise, the boundary conditions become,

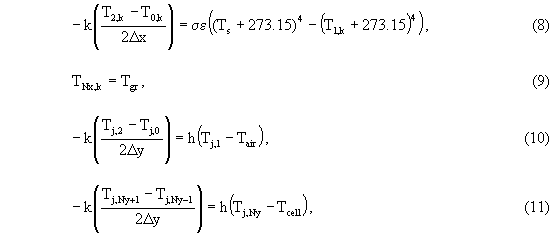
where j = 1 and j = Nx correspond to the x-coordinate boundary surfaces, and k = 1 and k = Ny correspond to the y-coordinate boundary surfaces. In the example application, discussed below, calculations are performed on a relatively coarse mesh of 20 mesh points in the x-direction and 11 mesh points in the y-direction.

In order to benchmark, or validate, the EXCEL solution, an alternate analysis was performed using the general purpose thermal conduction/radiation code MSC/THERMAL [11]. The wall in the application described below was modeled using the preprocessor in PATRAN. A total of 800 quadrilateral elements were used. The finite element mesh was refined in the high temperature gradient region near the steam pipe.

A bank of high-pressure steam lines passes through the north wall penetration of the Replacement High Level Waste Evaporator (RHLWE) at the Savannah River Site. The steam lines that pass through the wall penetration are not insulated. The steam lines rest on a W4X13 stainless steel I-Beam. This I-Beam rests on a stainless steel plate (part of the wall penetration) which is embedded in the concrete wall. There is concern that the high temperature (221 ^oC) steam pipes will heat the concrete around the penetration well above 93.3 ^oC (200 ^oF) and degrade its strength properties. However, if the depth of the temperature increase around the wall penetration is limited to a meter or so, the loss of concrete strength can be treated as local and the wall structural integrity will not be adversely affected. This calculation determines the temperature distribution around the penetration and in the wall under steady-state conditions. The arrangement of the steam lines and the wall penetration is shown schematically in Fig. 1. Note that the effect of the I-beam on the temperature distribution in the wall is neglected.

The concrete wall below the penetration is modeled as a two-dimensional slab. The wall is 10.668 m (35 ft) high and 1.0668 m (3.5 ft) thick. Any cylindrical effects due to the steam pipe are neglected. Due to the size of the wall, corrections due to the effects of curvature will be small. Further, since the thermal radiation will be emitted in all directions from the cylindrical surface of the steam pipe, the concrete wall above the penetration will behave similarly. Finally, it is assumed that the thermal radiation is emitted from a flat surface with normal incidence, that is, the effect of radiation view factors has been neglected. Including the radiation view factors will reduce the incident thermal radiation by correcting for the effects of cylindrical geometry and the opening into the evaporator cell.

Physical data used to solve Eqs. (7) through (11) are as follows:

1. T_s is 221 ^oC.
2. T_air is 38 ^oC.
3. T_gr is 38 ^oC.
4. T_cell is 60 ^oC.
5. k is 1.37 W/m-^oC. [8]
6. h is 4.5 W/m²-^oC (for free convection on a vertical plate). [9]
7. e is 0.63. [10]
8. s is 5.669´ 10^-8 W/m²-K⁴.

Figure 2 shows the results of the calculation for the temperature distribution in the wall beneath the penetration. As expected, the peak temperature is in the center of the wall at the x = 0 surface (203 ^oC) and the temperature drops to less than 93.3 ^oC in approximately 0.7 m. Likewise, the temperature across the wall (in the y-direction) shows approximately a 12 to 14 ^oC difference between the wall faces at y = 0 and y = 1.0668 m. This, of course, is due to the difference in the ambient gas temperatures on either side of the wall (T_air and T_cell). Indeed, the hot gas inside the cell (T_cell = 60 ^oC) actually heats the wall surface at y = 1.0668 m except for the top meter or so, where the influence of thermal radiation is most pronounced. Additional calculations performed assuming T_air = T_cell showed a symmetric temperature profile, as it should.

Figure 3 shows the temperature distribution resulting from first linearizing the radiation boundary condition, then solving the resulting linear problem. Notice the marked reduction in the peak temperature in the wall. This is a result of linearizing the radiation boundary condition. By assuming the temperature difference between the radiating body and the wall surface is small, the boundary condition may be written as,

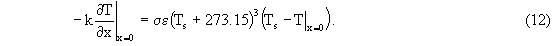
This will clearly reduce the influence of radiation on the temperature of the wall surface (at x = 0). Furthermore, since the peak temperature is reduced, the effect of natural convection cooling is more pronounced, as well.

Figure 4 shows the results of a comparison between the two ways of treating the radiation boundary condition. Interestingly, the largest temperature difference is near the boundaries at y = 0 and y = 1.0668 m. This is to be expected on physical grounds. Since the linearized boundary condition reduces the peak temperature on the boundary at x = 0, the natural convection cooling on the lateral surfaces of the wall (y = 0 and y = 1.0668 m) will have an increased effect, resulting in lower temperatures. This, in turn, leads to the increase in the temperature difference that is observed. Finally, it is interesting to note that approximately 2 m into the wall there is less than a 2 ^oC temperature difference. This, of course, is due to the low thermal conductivity of concrete.

From the comparison analysis using MSC/THERMAL, a peak temperature of 202.04 ° C was calculated along the surface as x = 0. The temperature drops to 93.3 ° C (200 ° F) at approximately 0.75 m from the upper surface of the wall near the steam pipe. The temperature contours are shown in Figure 5.

A desktop program has been developed in Microsoft EXCEL using Visual Basic for Applications (VBA) and applied to the analysis of a practical engineering problem. The two-dimensional steady state equation for heat conduction has been solved for a rectangular region subject to thermal radiation on one of its boundaries and natural convection cooling on its lateral surfaces. The final boundary was assumed to be at a constant temperature. The finite difference solution of this nonlinear problem using VBA showed good agreement with results from the commercially available finite element package, MSC/THERMAL (within 1%).

The authors gratefully acknowledge helpful discussions with B. J. Hardy of Westinghouse Savannah River Company. This work was performed under the auspices of the U. S. Department of Energy under contract DE-AC09-96SR18500.

1. M. Hagler, "Spreadsheet solution of partial differential equations," IEEE Trans. Educ. E-30 (1987) 130-134.
2. A. Kharab, "Use of a spreadsheet program in a two-dimensional heat conduction problem," Computer Methods in Applied Mechanics and Engineering 122 (1995) 173-181.
3. W. J. Orvis, Excel for Scientists and Engineers, 2^nd Edition, (Sybex: San Francisco, CA, 1996).
4. J. Walkenbach, EXCEL for Windows 95 Power Programming with VBA, 2^nd Edition, (IDG Books: Foster City, CA, 1996).
5. N. M. Ozisik, Boundary Value Problems of Heat Conduction, (Dover: Mineola, NY, 1989).
6. G. Dahlquist and A. Bjorck, Numerical Methods, (Prentice-Hall: Englewood Cliffs, NJ, 1974).
7. G. Golub and J. M. Ortega, Scientific Computing, An Introduction with Parallel Computing, (Academic Press: San Diego, CA, 1993).
8. J. P. Holman, Heat Transfer, 7^th Edition, (McGraw-Hill: New York, 1990). See Table A-3, p. 656.
9. J. P. Holman, Heat Transfer, 7^th Edition, (McGraw-Hill: New York, 1990). See Table 1-2, p. 13.
10. J. P. Holman, Heat Transfer, 7^th Edition, (McGraw-Hill: New York, 1990). See Table A-10, p. 667
11. MSC/PATRAN version 8.5, MacNeal-Schwendler Corporation, Los Angeles, CA 90041.

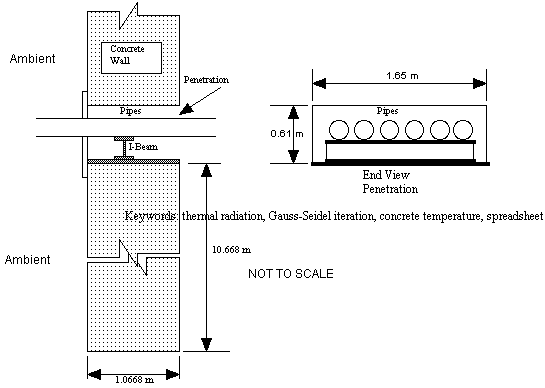
Figure 1. Schematic of concrete wall penetration

 

 

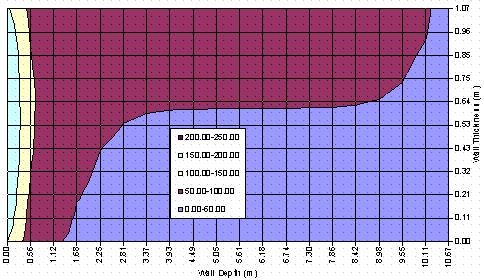
Figure 2. Temperature distribution for model problem

 

 

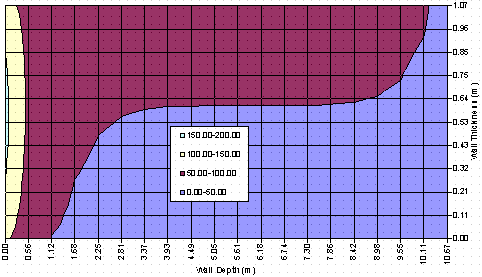
Figure 3. Temperature distribution for linear model problem

 

 

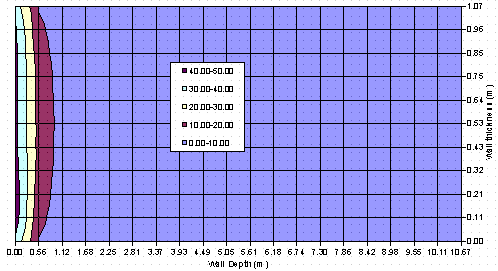
Figure 4. Temperature difference between linear and nonlinear model problems

 

 

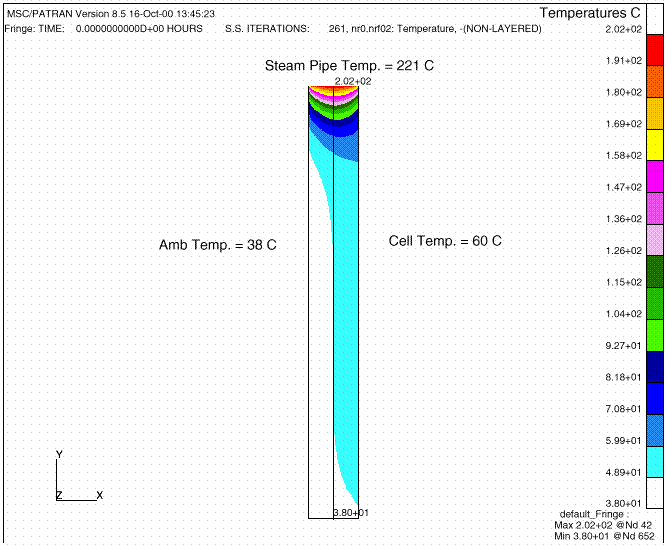
Figure 5. Temperature distribution from MSC/THERMAL