WSRC-TR-2001-00275
The Creation of an Historical Meteorological Database for Dose Reconstruction
Allen H. Weber, Robert L. Buckley, and Matthew J. Parker
Westinghouse Savannah River Company
Aiken, SC 29808
Richard P. Harvey and David M. Hamby
Oregon State University
This report was prepared as an account of work sponsored by an agency of the United States Government. Neither the United States Government nor any agency thereof, nor any of their employees, makes any warranty, express or implied, or assumes any legal liability or responsibility for the accuracy, completeness, or usefulness of any information, apparatus, product or process disclosed, or represents that its use would not infringe privately owned rights. Reference herein to any specific commercial product, process or service by trade name, trademark, manufacturer, or otherwise does not necessarily constitute or imply its endorsement, recommendation, or favoring by the United States Government or any agency thereof. The views and opinions of authors expressed herein do not necessarily state or reflect those of the United States Government or any agency thereof.
This report has been reproduced directly from the best available copy.
Available for sale to the public, in paper, from: U.S. Department of Commerce, National Technical Information Service, 5285 Port Royal Road, Springfield, VA 22161, phone: (800) 553-6847, fax: (703) 605-6900, email: orders@ntis.fedworld.gov online ordering: http://www.ntis.gov/support/ordering.htm
Available electronically at http://www.osti.gov/bridge/
Available for a processing fee to U.S. Department of Energy and its contractors, in paper, from: U.S. Department of Energy, Office of Scientific and Technical Information, P.O. Box 62, Oak Ridge, TN 37831-0062, phone: (865 ) 576-8401, fax: (865) 576-5728, email: reports@adonis.osti.gov
Abstract
Wind measurement towers did not exist at the Savannah River Site (SRS) until the early 1970s. Three relatively simple methods were used to create a 1955-61 meteorological database for the SRS for a dose reconstruction project. The winds were estimated from onsite measurements in the 1990s and National Weather Service (NWS) observations in the 1990s and 1950s using (1) a linear regression method, (2) a similarity theory approach, and (3) a simple statistical differences method. The criteria for determining success were based on (1) how well the mean values and standard deviations of the predicted wind speed agree with the known SRS values from the 1990s, (2) the shape of the predicted frequency distribution functions for wind speed, and (3) how closely the predicted windroses resembled the SRS windrose for the 1990s. The linear regression model’s wind speed distribution function was broad, flat, and skewed too much toward higher wind speeds. The similarity theory approach produced a wind speed distribution function that contained excess predicted speeds in the range 0-1.54 m s-1 (0-3 kts) and had "excluded" bins caused by predictions being made from integer values of knots in the NWS data. The distribution function from the mean difference method was smooth with a shape like a Weibull distribution and appeared to resemble closely the SRS 1992-96 distribution. The wind directions for all three methods of approach were successfully based on the mean difference method. It was difficult to discern differences among the wind roses produced by the three methods so the wind speed distribution functions need to be examined in order to make an informed choice for dose reconstruction.
1. Introduction
The Savannah River Site (SRS) has produced nuclear materials for the nation’s defense since the early 1950s. A dose reconstruction project to assess the effects of I-131 upon the SRS and its environs in the 1950s has been initiated by the Center for Disease Control (CDC). For modeling purposes, it is desirable to utilize meteorological data from the chosen time period, however, prior to this work meteorological data for the Savannah River Site (SRS) did not exist for the 1950s. The Savannah River Site’s meteorological monitoring program (Parker and Addis 1993) was not established until the early 1970s.
Efforts to create historical meteorological data can be rather complex and time consuming. One approach is to use sophisticated atmospheric models initialized with observations from surface observations and weather balloons. These models can then create hourly observations over large spatial grids (Stage et al. 1993). This implies re-running complex three-dimensional mesoscale or large-scale models to generate winds over entire years or decades and results in time-consuming computations (that do not necessarily provide more accurate results). In the case of the SRS, however, the reasonably close proximity of two National Weather Service (NWS) stations enabled the creation of an historical database using three different approaches that are described here. In a regression approach, statistical regression relationships between recent SRS and NWS databases for wind speed were determined and applied to archived NWS data to produce an SRS database for the desired time period. A second approach based on similarity theory was also used to generate wind speeds for the 1950s. In the similarity theory approach, wind speeds from the 10-meter NWS observations were extended to SRS’s 61-meter level (under an assumption of horizontal spatial homogeneity). Lastly, wind speed and wind direction estimates were obtained by finding mean differences between SRS and NWS stations during the 1990s and creating a set of corrections that were assumed to hold for the 1950s.
2. Methods
2.1 General Data Description
The locations of the wind measurement sites, terrain elevations for the region, and some land-use features are shown in Fig. 1. The land use in the South Carolina Piedmont is primarily agricultural broken by streams, forests and several small communities. The larger cities of Columbia, South Carolina, and Augusta, Georgia are separated by a distance of about 90 km.
Wind measurements are currently taken at the SRS and the NWS sites near the Columbia airport (CAE) and Augusta’s Bush Field (AGS). Although Columbia is roughly twice as far from the SRS as Augusta, the terrain surrounding the CAE measurement site is more similar to the SRS than the terrain around AGS. The main difference is that Bush Field lies in the Savannah River drainage basin near swampy terrain. Calms and fog occurrences are much more frequent at AGS than at CAE or at the SRS.
Wind measurements at the SRS and the NWS stations have important differences that are summarized in Table 1. Perhaps most important is that the measurement height at the SRS is 61 meters above ground level (AGL), while the NWS stations typically measure winds at 10 m AGL. In addition, the NWS instruments are much less sensitive than the SRS instrumentation, and the Bush Field data are subject to down-river flow due to the airport’s geographical location (Fig. 1). Finally, the NWS values are 2-minute averages at the top of the hour (i.e. almost a "snapshot"), whereas the SRS data are averaged continuously over one-hour intervals.
The first step in developing the desired statistical relationships was to obtain meteorological data from several nearby NWS stations for the appropriate time periods from the National Climatic Data Center (NCDC) (EarthInfo 1996; Brown 2001). Hourly observations of wind speed, direction, cloud cover, and cloud-height were archived by NCDC for NWS stations throughout the United States for the time periods of interest. Specifically, data from Bush Field in Augusta, Georgia (AGS) and Columbia, South Carolina (CAE) from 1955-1961 and 1992-1996 were selected to reconstruct winds at the SRS.
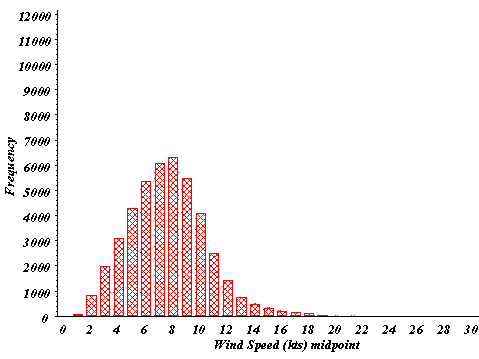
The wind speed frequency distributions for 1992-96 for SRS and the two NWS sites are shown in Figs. 2a-c. The SRS wind speed data in Fig. 2 were taken at the 61-m height with highly sensitive anemometers. The distribution resembles the theoretical Weibull distribution that is expected for accurate, continuous, long-term wind measurements (Krohn 1997). (Wind speed units of knots were used in the figures since the NCDC values are reported in whole knots).
The AGS and CAE frequency distributions, however, show spikes near zero reflecting the large number of wind speeds below the threshold of the NWS anemometer (recorded as a missing direction and a zero for wind speed). Indeed, an examination of the data showed that for the entire period 1992-96, virtually all the wind speeds below 1.54 m s-1 (3 kts) were entered as zeros for the NWS stations. To make the NWS distributions appear more realistic our collective experience in wind measurements was used to modify these zero entries for wind. All zero wind speed values were reassigned a random speed between zero and 1.54 m s-1 (3 kts) as follows: values between 1.03 and 1.54 m s-1 (2 and 3 knots) were assigned three times as frequently as values between zero and 0.257 m s-1 (0.5 knots), and values between 0.257 and 1.03 m s-1 (0.5 and 2 knots) were assigned twice as frequently as values between zero and 0.257 m s-1 (zero and 0.5 knots). The modified NWS wind speed distributions for the two sites are shown in Figs. 3a-b. The resulting CAE distribution appears reasonable, resembling a truncated Weibull distribution; the AGS distribution looks questionable with two maxima below 2.57 m s-1 (5 kts), as though far too many winds had been recorded as calm. Since the shape of CAE’s modified wind speed distribution function in Fig. 3 appeared to more closely resemble the SRS distribution in Fig. 2 than did the AGS distribution, the CAE wind speed data were given preference in the data reconstruction for SRS.
It was also determined that a significant percentage of the Bush Field wind direction data were missing for the periods of interest including the 1990s. This was mainly due to calm winds being reported, since Bush Field lies in the Savannah River drainage basin. The wind measurements at CAE had the advantage of being more complete as well as being collected over terrain more similar to the SRS than the AGS site, so CAE was given preference to represent wind directions for the SRS for the 1950s. To improve the percentage of direction data recovered for CAE, missing data for any given 1-hr period were substituted from AGS if available. This resulted in a gain of about 6% in data for CAE. Also, if Columbia data were missing for 1-hour, 2-hours, etc., or longer segments up to 8-hours, then persistence from the last known non-missing value was utilized. Performing these substitutions resulted in a gain of ~11.5% so that missing direction data was reduced to only about 0.5% in the final data set.
Table 2 shows the number of values and mean wind speed at the three sites (after the data substitution methods discussed above were implemented). Also shown is the number of values of non-calm wind direction measurements at the three sites.
The wind directions were then categorized into 16 compass sectors (22.5° bins) clockwise around the compass originating at north. The SRS data set and the improved CAE data set were merged into a single file with each record in the dataset denoting a different hour within the five-year period.
A comparison of wind direction data for both CAE and the SRS during the period 1992-96 was made to examine the similarities and disparities in the data. The SRS’s meteorological data for that period has undergone extensive checks for errors so it is viewed as the most reliable. The SRS’s 61-m windrose from H-Area for the five-year period 1992-96 is shown in Fig. 4a. Fig. 4b shows the CAE 10-m windrose for the same period. The CAE windrose has more frequent winds from the north than does the SRS windrose, and CAE lacks the frequent winds from the northeast that the SRS shows. Fig. 4c shows the AGS 10-m windrose for 1992-96. This windrose is nearly symmetrical when reflected about an E-W axis.
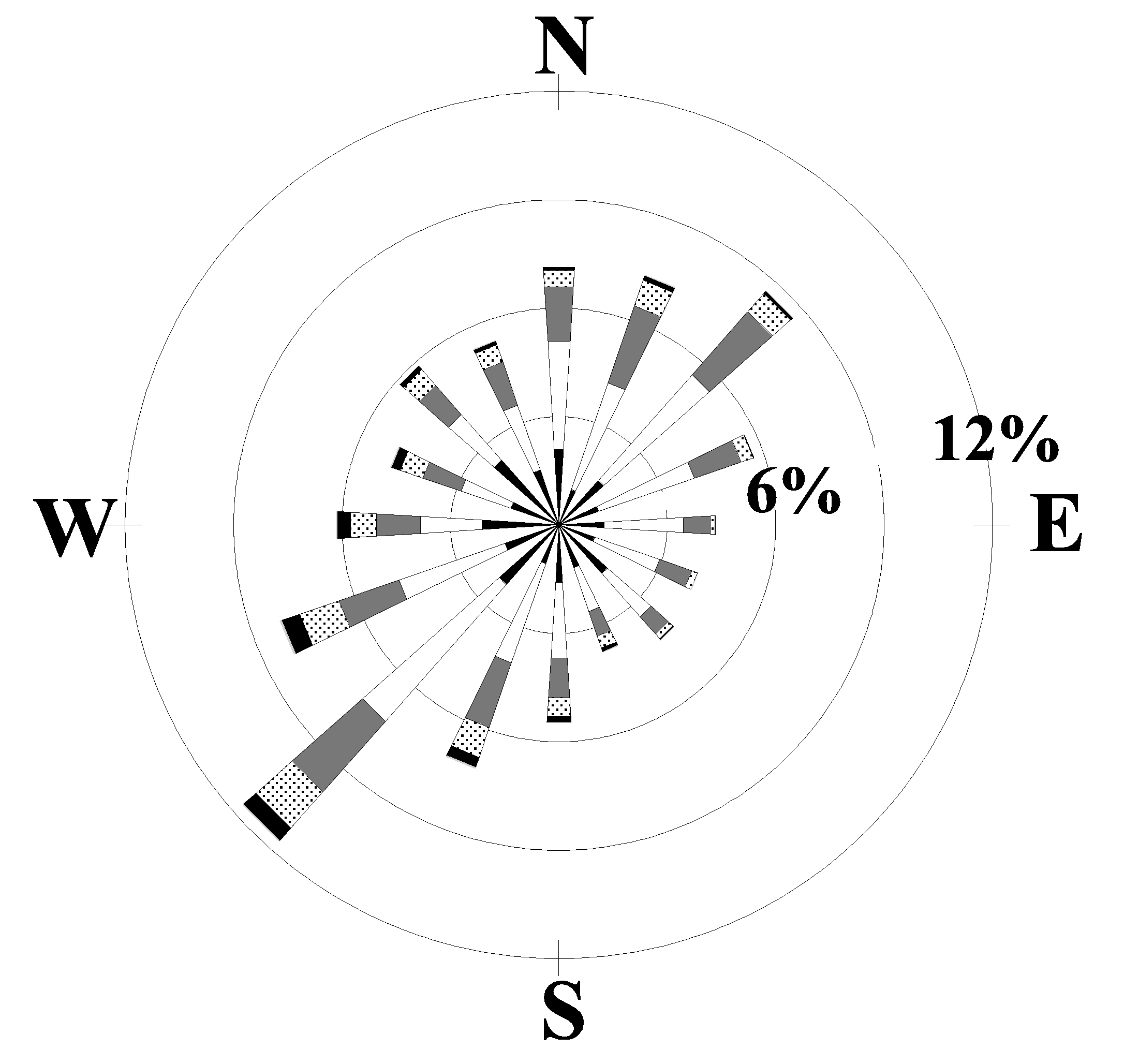
By examining the windroses for other time periods it can be determined whether the 1992-96 time interval for CAE resembles the long-term average. The windrose for CAE for the years 1948-95 is shown in Fig. 5a and the AGS windrose for the years 1949-95 is shown in Fig 5b. The windrose for CAE for the years 1955-61 is shown in Fig. 6a and the AGS windrose for the same period is shown if Fig 6b. It can be seen that the windrose for the total period of recorded data for CAE has many similarities to the windrose from SRS for 1992-96 shown in Fig. 4a. The predominant lobes are from the southwest and northeast directions with relatively few winds from the northwest and southeast. The forty-six year AGS windrose, however, shows a more nearly circularly symmetrical pattern.
In addition, the long-term windrose (1948-95) for CAE shows a much greater similarity to the 1955-61 CAE windrose in Fig. 6a (and the 1992-96 SRS windrose) than does the CAE windrose for the 1992-96 time period. In spite of the fact that the 1992-96 time period (as evidenced by the CAE windrose) is not representative of the longer-term means, it was nevertheless used to provide the basis for representing the wind direction for the SRS. All other reasonably close stations in the region (Athens, GA: AHN, Macon, Ga: MCN, Charlotte, NC: CLT, and Charleston, SC: CHS) were considered and rejected for various reasons, such as displaying orographic effects or for exhibiting climatologically different conditions than the SRS.
2.2 Regression Method
Regression equations for predicting the SRS wind speed for the 1955-61 time period from the CAE data during this same period were obtained using SASâ (1989) software procedures and the merged SRS and NWS 1992-96 data sets. Slopes and intercepts from the linear least-squares regression equations for wind speed were determined from the 5-year database for all seasons (4), sectors (16), and hours of the day (24) for a total of 1536 different sets. (The linear regressions were performed assuming the SRS speed as the independent variable with the CAE speed as the dependent variable. This choice was made due to the greater reliability, sensitivity, and accuracy of the SRS anemometers.) The Pearson correlation coefficient (SASâ , 1989) between the measured SRS speed and the measured CAE speed at this point was determined to be 0.391. This correlation coefficient does not indicate a particularly strong relationship between the dependent and independent variables, however the method can be applied rather easily to all 1536 different combinations cited above.
Data from the 1955-1961 time period for CAE (and AGS when needed) were then extracted and merged with the regression parameters determined from the 1992-1996 time-period. The sector definitions for the 1955-1961 data were based on CAE’s directions as before. The slope (Mreg) and intercept (Breg) for each of the 1536 combinations were then used to predict the SRS wind speed for the 1950s data set:
![]() (1)
(1)
where VSRS is the wind speed for the SRS and VCAE is the wind speed for Columbia.
At this point in the procedure the data were checked for glaring errors. In some cases, very small values of Mreg produced unrealistically large estimates of VSRS. If the predicted speed at the SRS exceeded 15 [m s-1], it was set identically equal to the CAE speed for that time. In addition, if the predicted speed was negative (which meant the regression procedure had failed to give a physically realistic result), it was set equal to the wind speed for CAE. Fortunately, the number of missing, negative wind speed predictions, and wind speeds greater than 15 [m s-1] from the improved CAE data set amounted to only 65 of 61368 cases (the number of hourly observations in the seven-year period).
2.3 Similarity Theory Method
A second approach was used to provide estimates of wind speed at 61-meters for the Savannah River Site using CAE observations based on dimensional analysis or "similarity theory". This approach was used to determine if it could offer improved wind speed estimates over the regression approach. Similarity theory applied over large horizontal distances has an underlying assumption of horizontally homogeneous turbulence. The horizontal homogeneity assumption is over the 90-km distance between SRS and CAE is questionable, but no other 61-meter wind speed measurement data are available in this region.
The similarity equations for wind speed in the constant flux layer are summarized by Panofsky and Dutton (1984) and repeated below for convenience. Similarity theory is based on dimensional analysis and begins with a length scale L, the Monin-Obukov length. The theory hypothesizes that the physical properties of the atmospheric surface layer can be specified in terms of the ratio of height above the surface z, and L where
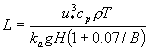 . (2)
. (2)
Here ![]() is the friction velocity (square root of the vertical turbulent momentum flux), cp is the specific heat at constant pressure, r is the air density, T is the air temperature, ka is the von Karman constant, g is the acceleration of gravity, H is the vertical turbulent heat flux, and B is the Bowen ratio. The Bowen ratio is the ratio of sensible to latent heat flux at the surface with values from about 0.1 to 5 depending on the surface.
is the friction velocity (square root of the vertical turbulent momentum flux), cp is the specific heat at constant pressure, r is the air density, T is the air temperature, ka is the von Karman constant, g is the acceleration of gravity, H is the vertical turbulent heat flux, and B is the Bowen ratio. The Bowen ratio is the ratio of sensible to latent heat flux at the surface with values from about 0.1 to 5 depending on the surface.
In similarity theory the non-dimensional wind shear S becomes a function of z/L as follows,
![]() (3)
(3)
where u is the mean wind speed in the boundary layer at some height z above the surface. The non-dimensional wind shear can be integrated to form the ![]() function where
function where
![]() (4)
(4)
and z is z/L, the variable of integration.
The ratio of wind speeds u1 and u2 at different levels z1 and z2 in the boundary layer is given by
![]() , (5)
, (5)
where z0 is the roughness length of the surface.
The function ![]() can be determined from
can be determined from![]()
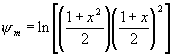 - 2 arc tan
- 2 arc tan
![]()
![]() (6a)
(6a)
and
![]()
for unstable conditions.
For stable conditions
![]() , (6b)
, (6b)
and for neutral conditions
![]() . (6c)
. (6c)
Golder (1972) determined estimates of L (or 1/L) from the Turner stability classes to use in cases where flux measurements are absent, such as an NWS monitoring station. In turn, the Turner stability classes can be estimated from time of day, cloudiness, and wind speeds measured near the surface. This stability class determination is discussed in detail in EPA-454/R-99-005 (2000) and summarized in the Appendix. In our application the CAE and AGS meteorological observations were used to determine the Turner stability classes. The estimates of 1/L given in Table 3 were obtained from Golder’s method assuming a roughness length z0 of 10 cm (since the instruments are located near airports with a few large roughness elements and terrain changes but where the grass and vegetation are kept reasonably short).
2.4 Wind Difference Method and Final Steps
Scalar averaged wind speeds (VDIFF) and vector averaged wind direction differences (qDIFF) were determined for each season (4), 22.5° sector (16), and hour of the day (24) between SRS and CAE for the 1992-96 time period. This made two sets of 1536 different corrections for each of wind speed and direction. The wind speed and direction prediction equations take the following form for each of the 1536 different subsets:
![]() , (7)
, (7)
![]() , (8)
, (8)
where VSRS and qSRS are the predicted wind speed and direction for SRS, and VCAE and qCAE are the wind speed and direction for CAE.
Stability class information is required to perform the dose calculations. The predicted value of wind speed, VSRS, along with the CAE (or AGS) observations of cloud height and total sky coverage are used to determine the Turner stability class, assuming the NWS measurements can be extrapolated to the SRS. As a final step, monthly joint frequency distributions for wind speed classes and 22.5° sectors were determined and formatted for utilization by dose assessment models.
3. Results
3.1 Mean Values and Standard Deviations for Predicted and Actual Wind Speeds
The mean values for wind speed for the two methods of determining wind speed described above are presented in Table 4. The predicted mean wind speeds for SRS are greater than the values for the 1990s data (compare with Table 2), however, the mean wind from CAE is also greater by about 11%. The linear regression method produced a larger wind speed value, and the value has a higher standard deviation. The mean difference method produced the closest value to the actual mean speed for SRS 1990s data. The correlation coefficient for the mean difference method was not calculated since the predicted values from this approach would be highly correlated due to the method that was used to obtain the values.
3.2 The Distribution Function of the Predicted Winds for 1955-61
The distribution functions for the predicted winds at the SRS for the years 1955-61 were determined for all three approaches. The actual CAE wind speed distribution for the years 1955-61 is shown in Fig. 7a. The regression result is shown in Fig. 7b, the similarity theory results are shown in Fig. 7c, and the difference results are shown in Fig. 7d. Fig. 7b for the regression result shows a very smooth distribution over the wind speed range with a relatively long tail at the higher speeds compared to the CAE distribution. Fig. 7b also shows too many wind speed values in the range 0-1.54 m s-1 (0-3 kts). Similarity theory (Fig. 7c) shows higher peaks in the mid-range of wind speed, but still has the long tail at the higher wind speed range and contains excess values in the range 0-1.54 m s-1 (0-3 kts). There are several "excluded" wind speeds, e.g., those at 4.63, 6.17, and 8.23 m s-1 (9, 12, and 16 kts). These are caused by the fact that the NWS winds are reported to whole knots that when entered into to the similarity equations produce identical values of speed, giving rise to the appearance of "excluded" wind speeds. The distribution function from the difference method shows the most reasonable distribution for the SRS predicted wind speeds.
3.3 Windroses Using Predicted Winds for the SRS 1955-61
Windrose plots for the predicted 1955-1961 SRS database were generated. Fig. 8 shows the predicted winds at SRS for 1955-61 using the three methods discussed. The predicted windrose for SRS in all three cases shows a good deal of similarity to the SRS windrose for 1992-96 and the windrose for CAE for 1955-61. Each windrose has strong lobes from the northeast and southwest that are what should be expected based on our earlier discussion.
3.4 Examination of the Residual Patterns of Wind Speed
In each of the three cases, plots of residuals versus actual wind speeds can be used to determine if the models are biased. The residuals are computed by taking the differences between the actual measured 1992-96 SRS wind speeds and the predicted wind speeds for each of the three models. Plots of residual wind speed as the ordinate and measured wind speed as the abscissa can show biases over the range of measured wind speeds if they exist. An unbiased model should show random scatter about a zero mean difference, a reasonably small range in the overall differences, no discernable slope to the pattern of points from left to right, and few, if any, outliers.
The residual plots are shown in Fig. 9 with identical axes for easy comparison. The regression model’s residual plot (Fig. 9a) has random scatter about zero, no discernable slope, a single outlier at +36 (not shown) and a fairly large range of –8 to +10 [m s-1]. The similarity theory model’s residual plot (Fig. 9b) shows an appreciable slope, no real outliers, and a range of –13 to +9 [m s-1]. The similarity theory residual plot shows bands of positively sloping lines caused by the fact that the wind speed observations are recorded in whole knots. Each wind speed in whole knots gives rise to a separate line in the plot. The difference model’s residual plot (Fig. 9c) has random scatter about zero, no slope, no outliers, and a range of –2 to +4 [m s-1]. These residual plot results show that among the three, the mean difference model is preferable.
4. Conclusions
Three relatively simple methods were used to create an historical meteorological database from onsite and nearby National Weather Service stations. The criteria for success are based on (1) the mean value and standard deviation of the predicted wind speed and how well these statistics agree with the known SRS values from the 1990s, (2) on the shape of the frequency distribution function for wind speed, and (3) on how closely the windrose resembles the SRS windrose for the 1990s.
The linear regression model produced a set of predictions that were plausible for the mean value and standard deviation, however the wind speed distribution function was skewed too much toward higher wind speeds. The distribution function also contained excess predicted speeds in the range 0-1.54 m s-1 (0-3 kts) whereas winds at the SRS’s 61-m measurement height do not favor these values. Overall the distribution function could be said to be too broad and flat to resemble the SRS distribution.
The similarity theory approach produced a set of predictions that again were plausible for the mean value and standard deviation, however the wind speed distribution function contained excess predicted speeds in the range 0-1.54 m s-1 (0-3 kts). The distribution function also contained "excluded" bins caused by predictions being made from integer values of knots in the NWS data.
The distribution function from the mean difference method was smoothly shaped, contained no excess values in the 0-1.54 m s-1 (0-3 kts) range and was not too broad nor flat to be realistic. The shape of the distribution also appears to resemble the Weibull distribution that careful wind measurements normally possess.
The residuals versus measured wind speeds plots for the three models showed that the difference method was preferable to the regression and similarity theory models. This was evidenced by the pattern of residuals having a random scatter about zero, no discernable slope over the range of measured wind speed, no outliers, and a fairly small range of –2 to +4 [m s-1] over the entire ensemble of points.
The dose reconstruction project does not depend heavily on the accuracy of individual hourly values of wind, but rather on the frequency distribution of the winds within the 16 compass sectors. Although any of the three methods may be adequate for the purpose of dose reconstruction estimates, the "best" statistical distribution for this purpose seems to come from the mean difference method because of its superior distribution function and lack of appreciable bias. Since this method produced the lowest mean wind speed it should also produce the most conservative dose predictions for the dose reconstruction project. The mean difference method is also the simplest of the three methods to implement.
The wind directions for all three methods of approach were based on the mean difference method. The mean difference method produced windroses for all three cases that were very close to the expected windrose shape (SRS’s 1990s windrose, Fig. 4a). It was felt that this was an important result that greatly simplifies the task of providing wind direction data for a site such as SRS where no measurements were being taken in the time period of concern. Close examination of each of the windroses produced by the three methods shows that the differences among them are difficult to discern so attention must be given to the wind speed distribution functions to be able to make an informed choice among the methods for dose reconstruction.
References
Table 1: Known difference between the winds measured
at the National Weather Service, Augusta, Georgia (AGS)
Columbia, South Carolina (CAE) and the Savannah River Site (SRS).
|
Difference |
SRS |
CAE |
AGS |
|
Height of Sensors |
61-m |
10-m |
10-m |
|
Instrument Sensitivity |
High sensitivity |
Robust instrumentation, but low sensitivity. |
Robust instrumentation, but low sensitivity. |
|
Averaging Time |
1-hour (continuous) |
2-minute ("snap-shot") |
2-minute ("snap-shot") |
|
Topographical Influences |
Pine tree forest. Mostly flat within 2.0 km of the tower. Modest terrain changes beyond. |
Airport location. |
Airport location. |
Table 2: Mean wind speeds and directions (after data substitution methods
were implemented) with standard deviations for the 1992-96 time period.
CAE and AGS measurements are at 10-m heights; the SRS measurement is at
61-m height. (Missing wind directions are mainly the result of calm conditions).
|
Number of values |
Mean |
Std. Dev. |
|
|
SRS Speed m s-1 |
43848 |
3.94 |
1.50 |
|
CAE Speed m s-1 |
43848 |
2.99 |
1.90 |
|
AGS Speed m s-1 |
43846 |
2.73 |
1.94 |
|
SRS Direction |
43848 (100%) |
||
|
CAE Direction |
36164 (82.5%) |
||
|
AGS Direction |
31293 (71.4%) |
Table 3: Values of 1/L for various Turner stability classes
that were used to extrapolate 10-m wind speeds to 61-m heights.
|
Turner stability class |
Value of 1/L for CAE |
|
A (1) |
-0.108 |
|
B (2) |
-0.060 |
|
C (3) |
-0.025 |
|
D (4) |
0.0 |
|
E (5) |
0.05 |
|
F (6) |
0.022 |
|
G (7) |
0.06 |
Table 4: Mean speeds and standard deviations for the 1955-61
time period.
CAE measurements are at 10-m heights; the SRS predicted wind speed is for the
61-m height.
|
Speed Type and Location |
No. of values |
Mean [m s-1] |
St. dev. [m s-1] |
|
CAE observed |
61368 |
3.34 |
2.12 |
|
SRS predicted |
61368 |
4.58 |
3.18 |
|
SRS predicted |
61368 |
4.80 |
2.84 |
|
SRS predicted |
61271 |
4.26 |
1.93 |
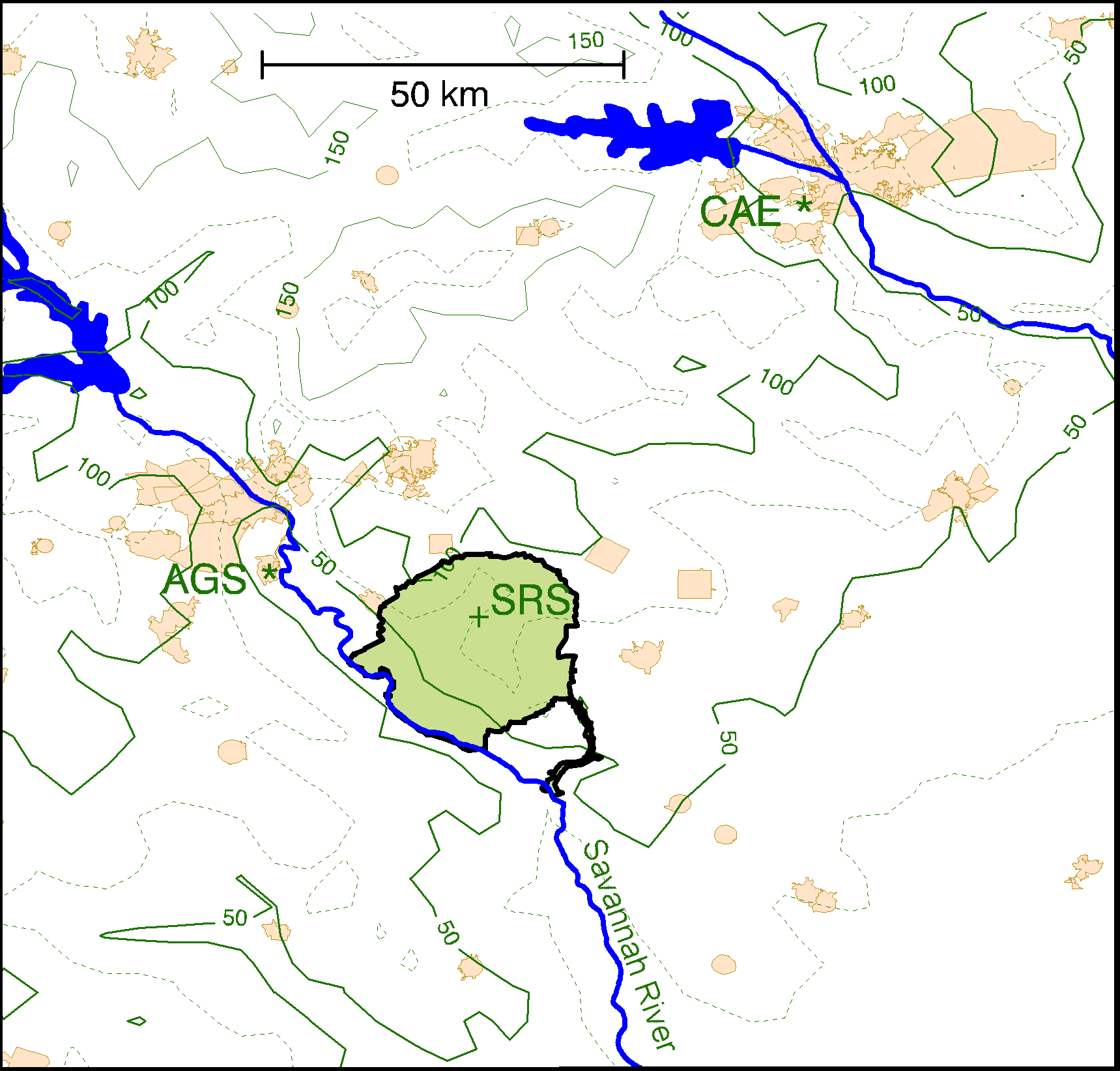
Figure 1: Map of the Savannah River Site (SRS) area with Augusta Bush Field
(AGS)
to the northwest and Columbia airport (CAE) in the northeast corner. Topographic
contours are at 25 m
(above sea level) intervals with 50 and 100-m levels highlighted. Lighter shaded
filled areas are cities or towns.
(a) SRS
(b) CAE
(c) AGS
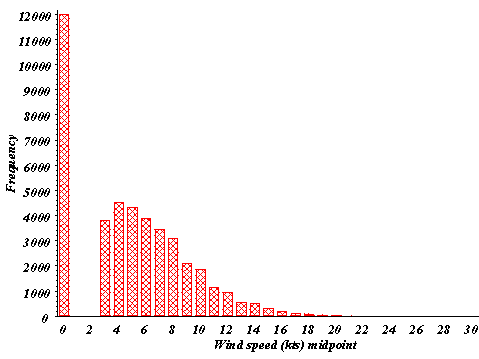
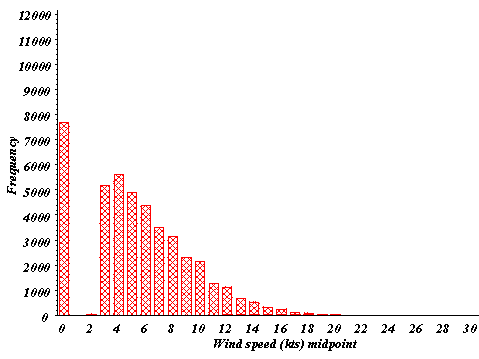
Figure 2: Wind speed frequency distributions for 1992-96 for
(a) SRS, (b) CAE, (c) AGS. Wind speed units of knots are used
for clarity since the NWS reports wind speed to the nearest knot.
(a) CAE
(b) AGS
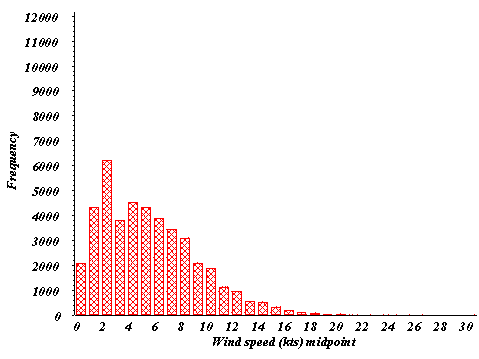
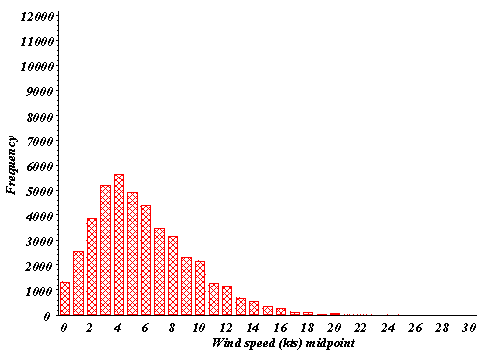
Figure 3: Modified wind speed frequency distributions for
1992-96 for (a) CAE, (b) AGS. Modifications were performed on the
calms of Fig. 2 to distribute them in the range 0-3 knots. Wind speed units of
knots are used for clarity since the NWS reports the wind speed to the nearest knot.
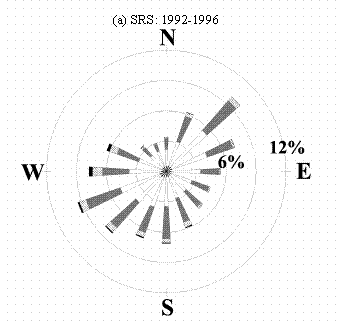
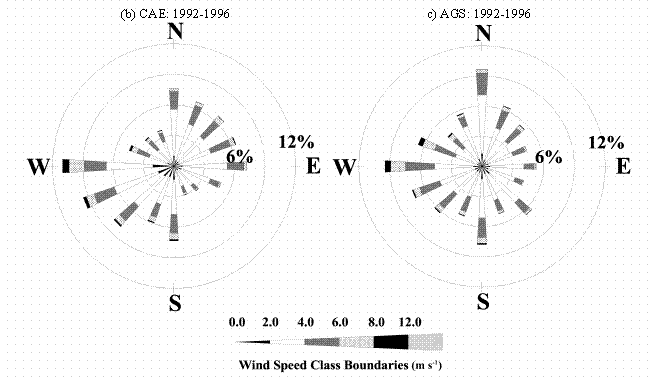
Figure 4: Windrose plots for the years 1992 to 1996 for
(a) SRS, (b) Columbia, SC, (c) Augusta, GA. The windrose plots depict the
frequency of the direction from which the wind is blowing and the wind speeds.
(a) CAE: 1948-1995
(b) AGS: 1949-1995
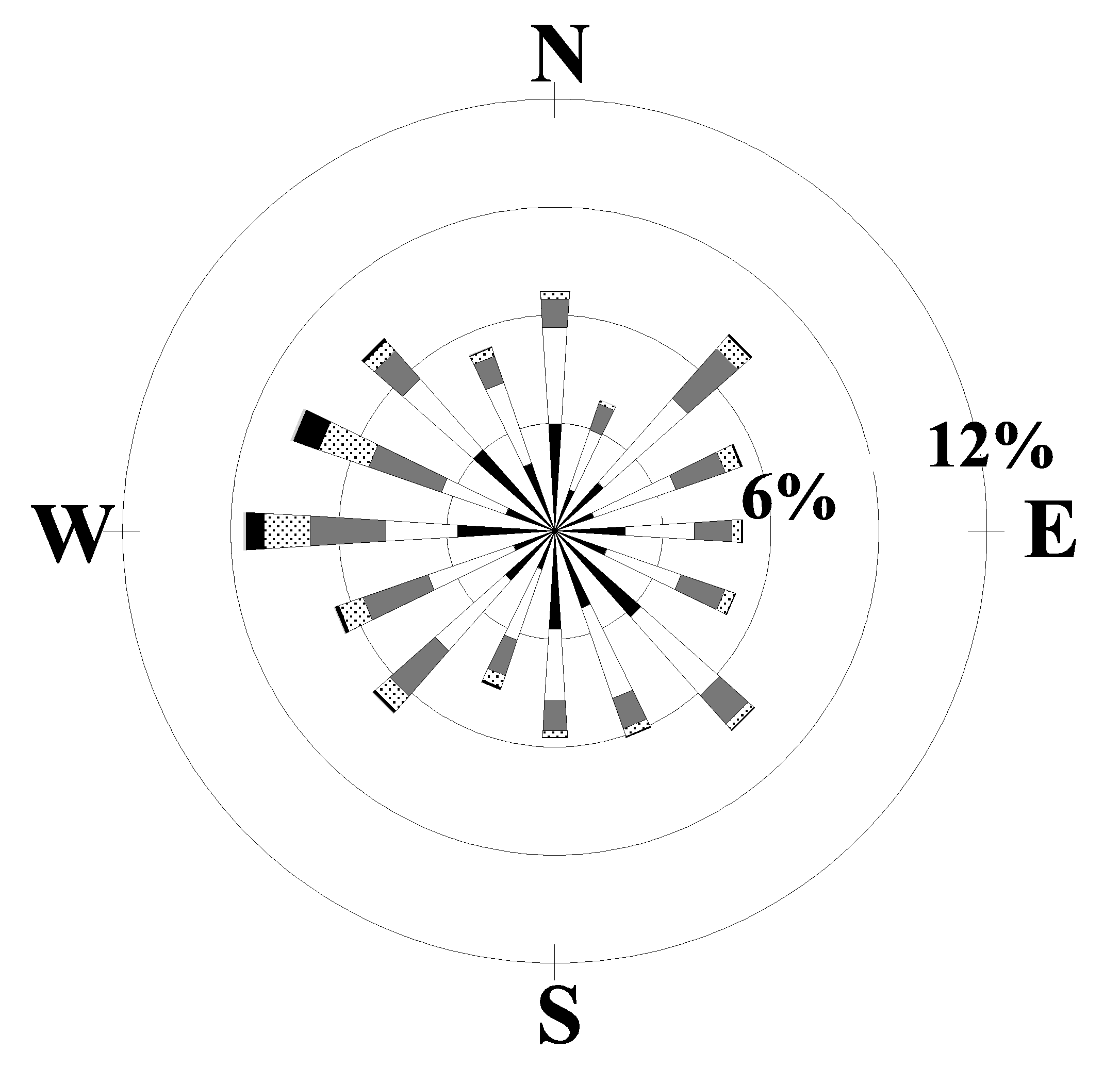

Figure 5: Windrose plots for the late 1940s to 1995 for
(a) Columbia, SC, (b) Augusta, GA. The windrose plots depict the
frequency of the direction from which the wind is blowing and the wind speeds.
(a) CAE: 1955-1961
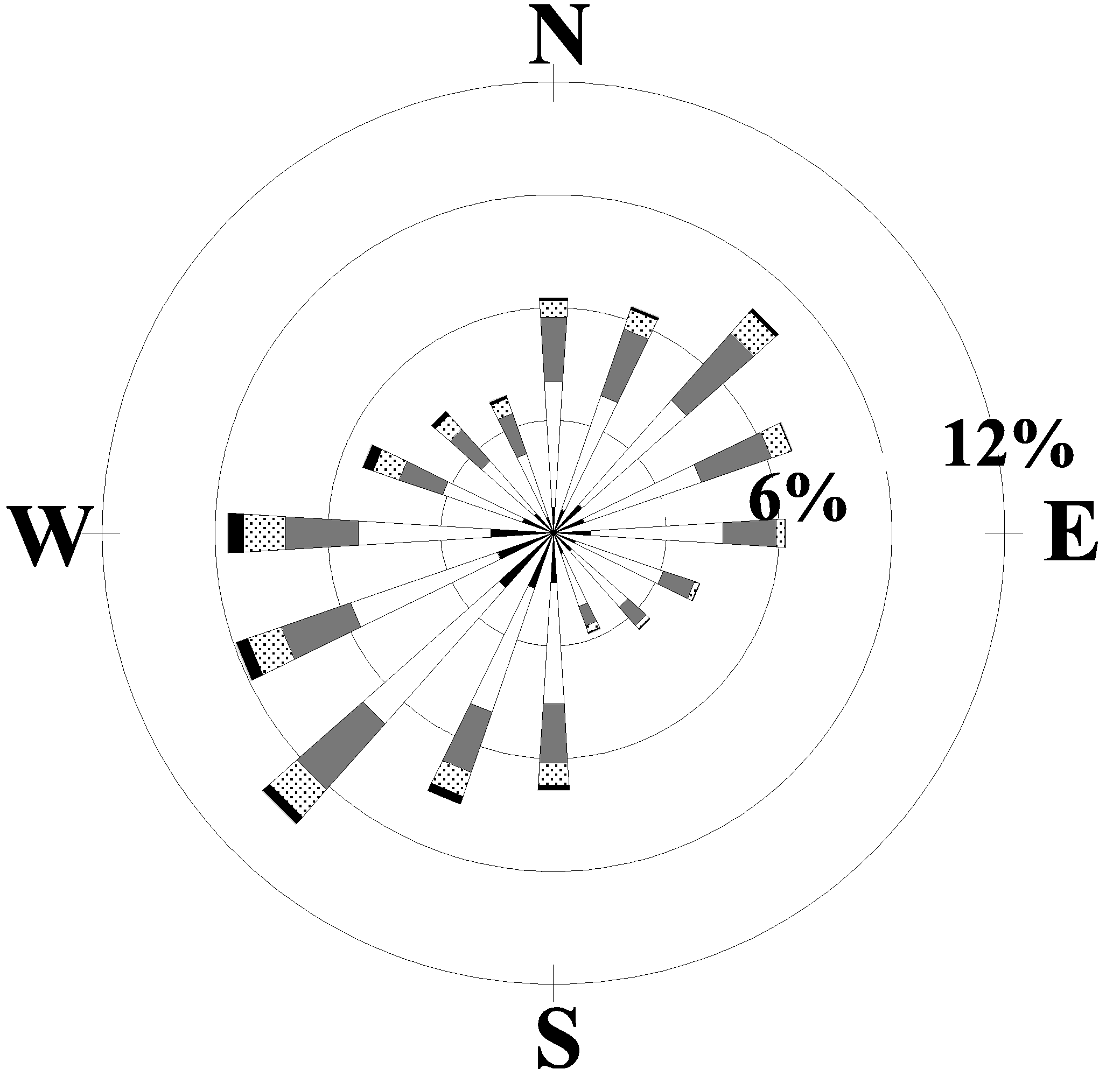
(b) AGS: 1955-1961
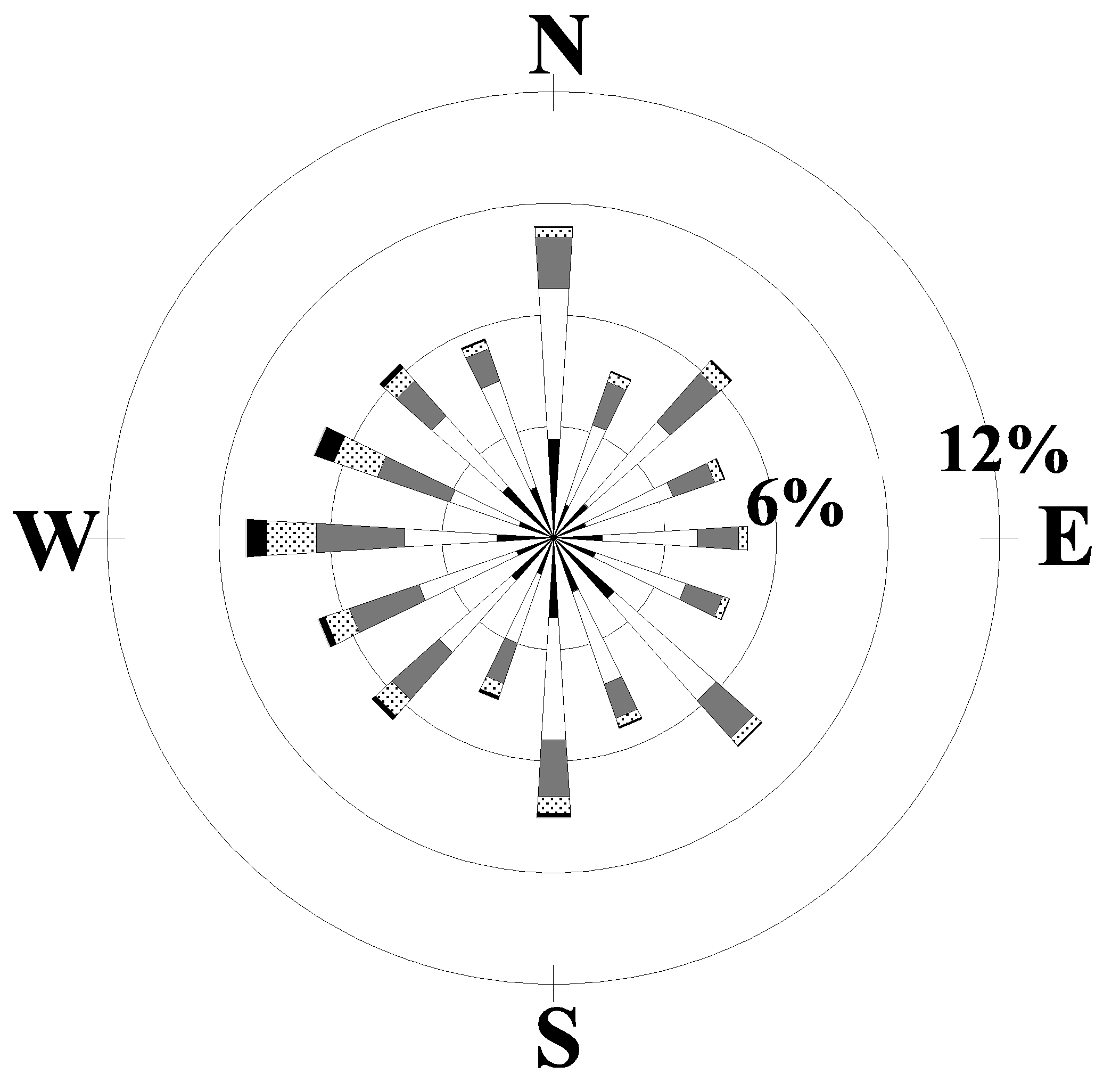

Figure 6: Windrose plots for the years 1955 to 1961 for
(a) Columbia, SC, (b) Augusta, GA. The windrose plots depict the
frequency of the direction from which the wind is blowing and the wind speeds.
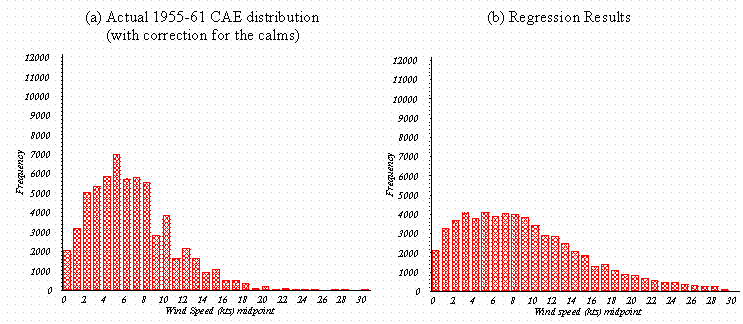
Figure 7: Wind speed distribution functions for (a) the improved CAE 1955-61 data,
(b) the linear regression predictions (c) the similarity theory predictions, and
(d) the mean difference method predictions.
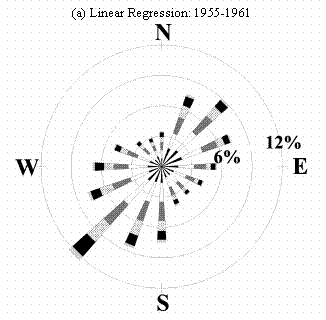
Figure 8: Windrose plots as derived for the SRS for the years
1955 to 1961 using
(a) Linear regression, (b) similarity theory, (c) mean differences. The windrose
plots
depict the frequency of the direction from which the wind is blowing and the
wind speeds.
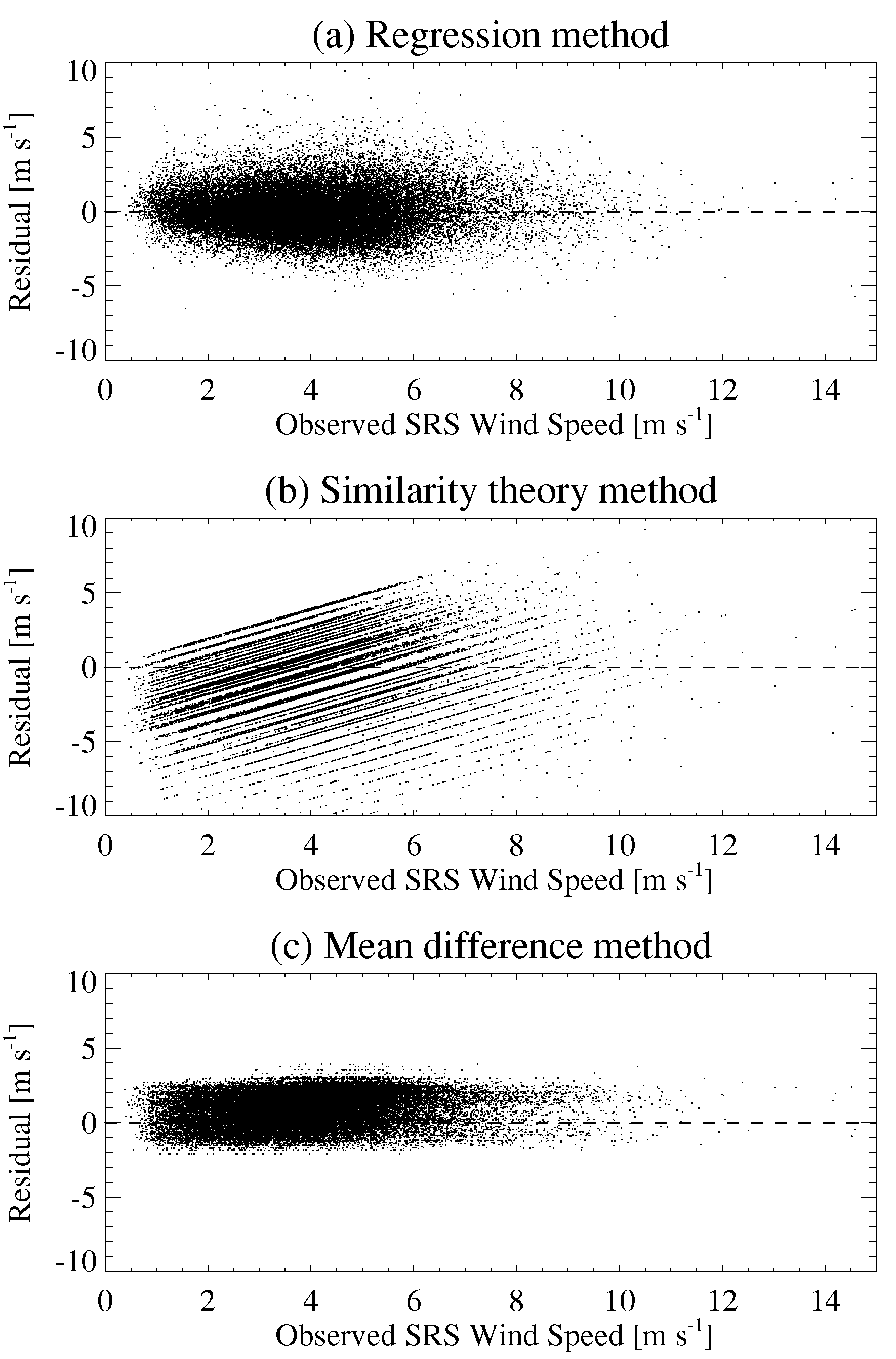
Figure 9: Scatter plots of observed wind speed at SRS for 1992-96 versus the residual for the
(a) regression method, (b) similarity theory method, and (c) mean difference method
Appendix: Determination of Stability Class
The atmospheric stability is important in determination of lateral and vertical horizontal dispersion parameters. The most commonly used classification is that of Pasquill (1961), later modified by Gifford (1961), and referred to as the Pasquill-Gifford (P-G) stability class. Unstable conditions are represented by the letter ‘A’ (or the number 1), while increasingly more stable conditions are denoted with successive letters of the alphabet, such that extremely stable conditions are represented by ‘F’ and/or ‘G’ (6 and/or 7). Neutral atmospheric conditions are given by the ‘D’ (4) classification. Turner (1964) devised a scheme for determining the stability class of the atmosphere using data customarily collected at NWS sites by considering radiative and wind speed effects. Net radiation calculations require knowledge of total cloud cover, ceiling height and solar altitude (itself a function of the time of day and year, as well as geographic location). The following tables, reproduced from EPA-454/R-99-005 (2000), provide the mechanism for determining the P-G stability classes.
The solar altitude, q, is the angle the sun makes with respect to the earth’s surface. When the sun is directly overhead (i.e. ‘high noon’), q = 90° leading to the strongest insolation, while weak insolation occurs when the sun is near the horizon. This angle is uniquely determined from the latitude and longitude of the location of interest, the time of day, as well as the time of year. Once determined, an insolation class number (IN) is defined, as given in Table A.1.
The Pasquill-Gifford stability categories (A through G) as a function of wind speed and net radiation index (NRI) are shown in Table A.2. Once the solar altitude and insolation class number are known (Table A.1), the procedure shown in Table A.3 requiring the total cloud cover (TC) and ceiling height (CH) is used to determine the NRI. Knowing the NRI and wind speed for a given time yields the P-G stability class (Table A.2).
Table A.1: Insolation class number (IN)
as a function of solar altitude, q.
|
Solar Altitude (°) |
Insolation |
IN |
|
60 < q |
Strong |
4 |
|
35 < q £ 60 |
Moderate |
3 |
|
15 < q £ 35 |
Slight |
2 |
|
q £ 15 |
Weak |
1 |
Table A.2: Turner’s conversion from NRI to stability class.
|
Wind speed |
Net Radiation Index (NRI) |
|||||||
|
[m s-1] |
[knots] |
4 |
3 |
2 |
1 |
0 |
-1 |
-2 |
|
0 to 0.7 |
0, 1 |
A |
A |
B |
C |
D |
F |
G |
|
0.8 to 1.8 |
2, 3 |
A |
B |
B |
C |
D |
F |
G |
|
1.9 to 2.8 |
4, 5 |
A |
B |
C |
D |
D |
E |
F |
|
2.9 to 3.3 |
6 |
B |
B |
C |
D |
D |
E |
F |
|
3.4 to 3.8 |
7 |
B |
B |
C |
D |
D |
D |
E |
|
3.9 to 4.8 |
8, 9 |
B |
C |
C |
D |
D |
D |
E |
|
4.9 to 5.4 |
10 |
C |
C |
D |
D |
D |
D |
E |
|
5.5 to 5.9 |
11 |
C |
C |
D |
D |
D |
D |
D |
|
³ 6.0 |
³ 12 |
C |
D |
D |
D |
D |
D |
D |
Table A.3: Procedure to determine net radiation index (NRI).
