
WSRC-MS-99-00958
Evaluation of Methods for Estimating the Uncertainty
of Electronic Balance Measurements
J. P. Clark
Westinghouse Savannah River Company
Aiken, South Carolina 29808
This report was prepared as an account of work sponsored by an agency of the United States Government. Neither the United States Government nor any agency thereof, nor any of their employees, makes any warranty, express or implied, or assumes any legal liability or responsibility for the accuracy, completeness, or usefulness of any information, apparatus, product or process disclosed, or represents that its use would not infringe privately owned rights. Reference herein to any specific commercial product, process or service by trade name, trademark, manufacturer, or otherwise does not necessarily constitute or imply its endorsement, recommendation, or favoring by the United States Government or any agency thereof. The views and opinions of authors expressed herein do not necessarily state or reflect those of the United States Government or any agency thereof.
This report has been reproduced directly from the best available copy.
Available for sale to the public, in paper, from: U.S. Department of Commerce, National Technical Information Service, 5285 Port Royal Road, Springfield, VA 22161, phone: (800) 553-6847, fax: (703) 605-6900, email: orders@ntis.fedworld.gov online ordering: http://www.ntis.gov/support/ordering.htm
Available electronically at http://www.osti.gov/bridge/
Available for a processing fee to U.S. Department
of Energy and its contractors, in paper, from: U.S. Department of Energy, Office
of Scientific and Technical Information, P.O. Box 62, Oak Ridge, TN 37831-0062,
phone: (865 ) 576-8401, fax: (865) 576-5728, email: reports@adonis.osti.gov
Abstract
International and national regulations are requiring testing and calibration laboratories to provide estimates of uncertainty with their measurements. Many balance users are having questions about determining weight measurement uncertainty, especially if their quality control programs have provided estimates of measurement system "bias and precision". Part of the problem is the terminology used to describe the quality of weight and mass measurements. Manufacturer’s specifications list several performance criteria, but do not provide estimates of the "uncertainty" of measurements made using an electronic balance. Several methods for estimating the uncertainty of weight and mass measurements have been described in various publications and regulations in recent years. This paper will discuss the terminology used to describe measurement quality, i.e. "accuracy", "precision", "linearity", "hysteresis", "measurement uncertainty"(MU) and the various contributors to MU and will discuss the advantages and limitations of various methods for estimating MU. The methods include using:
Examples of each will be discussed.
Introduction
Electronic balances have become so sophisticated that many calibrate themselves and appear to provide "error free" measurements. However, this is not the case. All measurements have error that obscures the true value. The error creates uncertainty about the quality of the measured value. For a measurement to have value, it should have an estimate of the magnitude of error associated with it. An estimate of the error allows the user to evaluate the quality of the measurement. However, many measurement generating organizations have questions about determining accurate estimates of the uncertainty associated their weight measurements.
The metrological community recognized the need for standardization in the area of measurement uncertainty (MU) over 20 years ago and developed standards and guides on the subject. Generally speaking, industrial calibration and testing organizations have lagged behind in reaching the same levels of understanding and implementation attained by legal and scientific metrology communities. They are being required to catch up, if they want to participate in international business. The specific area of weighing has its MU concerns. Much has been written about the sources of error in weighing equipment, methods for controlling error, and methods for estimating the uncertainty of weight measurements. The author is unaware of any consensus about the best method for determining estimates of weight MU. This paper will review the sources of error and methods that are currently being used to "estimate" MU.
Background
The author’s organization calibrates more than 400 scales and balances at a government owned company operated site near Aiken, SC called the Savannah River Site (SRS). Regulations and the site quality assurance program require all balances to be calibrated routinely with standards traceable to the national standards. Many of the site operations have quality control programs, which require operators to satisfactorily weight two or more standards on a balance before making process measurements. Control charts are often used to record and evaluate the QC measurements. Biases are determined by subtracting the measurement means from the reference values of the mass standards. The variance of the measurements is used to estimate the precision of the balance. Locally, bias and precision statistics have been considered the MU information for balances.
The site also requires measuring and test equipment (M&TE) to be calibrated with standards having ¼ the uncertainty of the M&TE. Since weighing equipment specifications do not include "uncertainty", many users look at the specifications (see Table 1) to find something similar and often use the standard deviation (s) of the repeatability as the uncertainty. This can cause a problem if the person calibrating the balance tries to ratio the balance standard deviation to a weight certificate’s uncertainty statement.

Weighing is considered one of the simplest measurements in the laboratory or production facility. Procedures are required for all operations and provide basic techniques of operation and care, but do not specifically address MU. Balance operator training covers good laboratory practices and basic principles for weighing. However, MU is not usually addressed.
The importance of measurement quality is increasing. Measurement users are now requesting "uncertainty estimates" from measurement providers, rather than bias and/or precision estimates. This has caused some confusion as the producers discover MU is more than "bias and precision" estimates. Many balance operators are unaware of the vast amount of information metrologists have developed about every facet of weight and mass measurements.
Much of that information has been distilled and published in literature available from balance manufacturers. Two such publications are quoted below in defining some of the measurement quality terminology associated with weighing and manufacturers specifications. Many of the definitions are similar to those in the international standards, but have been adapted to weight or mass measurements. A good understanding of the basic terminology is essential in evaluating MU estimation methods.
Weight Measurement Terminology
The Sartorius Corporation’s publication, Fundamentals of Weighing Technology (Terms, Methods of Measurement, Errors in Weighing) is an excellent reference. That publication provides the following explanations for some of the terminology used to describe various aspects of weight measurement quality.i
Accuracy: This is only a qualitative concept that defines the metrological extent to which the weight readouts of a weighing instrument approach the true values of the quantities being weighed. Accuracy is quantified by a weighing instrument's readability, standard deviation, resolution, accuracy class or the uncertainty of measurement. (Calibration certificate)
Hysteresis: Hysteresis means that at a constant load, the displayed value depends on the previous load. Quantitatively, hysteresis is expressed as the difference between the readouts obtained when the same load is weighed once following a lighter load and once following a heavier load. In terms of weighing instruments, hysteresis occurs particularly with strain-gauge load cells and weighing instruments subject to mechanical friction.
Linearity error: Also referred to in the specifications as linearity". This is the deviation from the theoretically straight-lined (linear) slope of two interdependent values. For weighing instruments, this means the positive or negative deviation of the readout from the actual load on the pan, when the zero point and the span have been correctly adjusted.
Repeatability: The ability of a weighing instrument to display corresponding results under constant testing conditions, when the same load is repeatedly place onto the weighing pan in the same manner. In general, the standard deviation or the difference between the largest and the smallest result for a defined number of measurements is used to specify this quantity.
Standard Deviation: A mathematic quantity for evaluating
a weighing instrument in terms of its reproducibility or repeatability:
The standard deviation "s" is defined as:

To determine the standard deviation with sufficient certainty,
the number of times the measurement is repeated must be high enough (at
least ³ 6)
Uncertainty (of measurement): The uncertainty of measurement "u" specifies the range for a measured value, within which the unknown, error-free result lies, usually with a statistical uncertainty of 95%. (This corresponds to u = 2s). An example of a weighing result expressed along with the uncertainty of measurement: M = (394.27 ± 0.02) g
A second publication that provides a more comprehensive list of definitions of weighing terminology is the Mettler-Toledo Glossary of Weighing Terms (A Practical Guide to the Terminology of Weighing). It is the source of the following definitions.ii
Precision: Only a qualitative term as a judgment regarding the metrological features of a balance. A better designation would be Tolerance Limits, ® Standard deviation, ® and Uncertainty. (When the symbol (® ) is used, that term is defined else where.)
Reproducibility: Extent of the approximation between the results of measurements of the same measured variable with the individual measurements being performed under different conditions with regard to, e.g.
Notes: 1. A valid statement of reproducibility
requires specification of the different conditions.
2. The reproducibility can
be specified quantitatively by the result scatter.
Uncertainty of measurement: The uncertainty in the
measurement of a result always includes the random errors (mathematically
express by the ® Standard Deviation or the
® Confidence Interval) of all individual
variables, which are used to calculate the ®
Measurement Result, as well as systematic errors, which have not been determined
because they cannot be measured and can therefore only be estimated. It
is always presupposed that those systematic errors that have been determined
have also been corrected. Basically, the result of a weighing series "y"
consisting of "n" individual weighings should be as follows:
Y = XbarE ± uWhere XbarE is the mean error that is no longer afflicted by the detected systematic errors (e.g. air buoyancy) and "u" is measured uncertainty.
These weighing technology terms will be referred to later in this paper. Additional terminology excerpts from the GUM are listed to facilitate the evaluation of the different methods of estimating weight MU.
Classification of Components of Uncertaintyiii
In general, terms that are specific to this Guide are defined in the text when first introduced. However, the definitions of six of the most important specific terms are given here for easy reference.
2.3.1 standard uncertainty uncertainty of the result of a measurement expressed as a standard deviation
2.3.2 Type A evaluation (of standard uncertainty) method of evaluation of a standard uncertainty by the statistical analysis of a series of observations
2.3.3 Type B evaluation (of standard uncertainty) method of evaluation of a standard uncertainty by means other than the statistical analysis of a series of observations.
23.4 combined standard uncertainty standard uncertainty of the result of a measurement when that result is obtained from the values of a number of other quantities equal to the positive square root of a sum of terms, the terms being the variances or covariances of these other quantities weighted according to how the measurement result varies with changes in these quantities
2.3.5 expanded uncertainty quantity defining the interval about the result of a measurement, within which the values that could reasonably be attributed to the measurand may be expected to lie with a high level of confidence
NOTES
2.3.6 coverage factor numerical factor used as a multiplier of the combined standard uncertainty in order to obtain an expanded uncertainty.
NOTE - A coverage factor, k, is typically in the range 2 to 3.
Precision is general term that encompasses the concepts of repeatability and reproducibility. There is an important distinction between repeatability and reproducibility that could have a monumental affect on the estimate of uncertainty. Repeatability defines the variability observed at one point in time by one operator recording a series of readings from placing one object on a balance several consecutive times. The standard deviation of this collection of measurements captures the rounding error and the ability of the balance to repeat the same "reading". Reproducibility defines the variability of a measurement system in measuring the same standard or object over a long period of time, under different environmental conditions and with different operators. All of these variables can contribute error to the measurement and expand the uncertainty. Since measurements are collected over a long period of time, the standard deviation of the average measurement will include the environmental affects. The first two methods that are used to estimate uncertainty use the repeatability statistic, rather than a reproducibility statistic. This will be seen later.
Quality Weighing
Prior to determining uncertainty of weight measurements the quality requirements must be established. Several activities or programs should be in place. They include the following:
Weighing System Components
After determining the accuracy / uncertainty requirement and selecting the appropriate electronic balance the other requirements for quality weighing must be considered. The best way to do this is to look at everything that is involved in making the measurement. In addition to the balance, the standards, environment, operator, procedure and material being weighed make up the measurement system. Each can contribute to the uncertainty of weight measurements. Within each component of the measuring system are potential sources of error that can make the measured weight uncertain. Each component has some error associated with it. However, there are usually less than 6 components that contribute >90% of the uncertainty to a measurement. Listing the components and estimates of the amount of error they each could contribute to the MU is considered an error budget.
The construction of a table of components that affect measurement quality is the first step in establishing an error budget. This requires an in depth knowledge of the measurement system and/or investigative effort to quantify each contributor. This is an uncertainty analysis. The ultimate objective is to combine them into one statistic that estimates MU.
Table 2 is an example of a typical weight measurement system. This list has 5 main components in a system that involves making direct measurements. Other lists might contain the procedure or method used to make measurements. For example direct, indirect or substitution weighing.
In making weight or mass measurements, an unknown object’s weight is directly or indirectly compared to the known weight of a stainless steel standard or the force equivalent. The standards have uncertainty that is transferred to all the measurements made against them. This fact is the basis for guidelines or regulations that require using calibration or check standards having uncertainties that are much smaller than the measuring instrument. Variation in each of these components produces random and/or systematic variation in the measurand that causes uncertainty. To make the most accurate measurements, ways must be found to minimize the sources of random and systematic variation that affect the accuracy / uncertainty of the measurand.
After the sources of variation are minimized it is still necessary to know the magnitude of the MU. Reliable estimates of MU allow users to determine if a measurement system is fit for its intended use.
Figure 1 shows a tank calibration being performed on trailer mounted industrial balance outside on a warm day. The balance operator is using 50-pound class F weights on a balance having 10,000 scale divisions. Many sources of error in the measurement system components will determine the final measurement uncertainty.

There are at least 3 methods currently being used to estimate weight MU. The three include: doing a type B uncertainty analysis, designing experiments or performing balance calibrations to empirically determine estimates; or determining estimates from measurement control program data and calibration certificates.
Method 1: Manufacturer’s Specifications
Most manufacturers’ specifications list several performance criteria, but do not provide estimates of the balance "uncertainty" or accuracy. Balance users often use the standard deviation of the repeatability as the "uncertainty" of the balance. In specifying accuracy requirements for weighing, some authors have used s as a basis of calculating the minimum number of scale intervals allowed to attain a certain confidence level. Using the repeatability s as an estimate for MU fails to include the contributions from the other error sources given in a balance specification. See Table 1. All of the performance specifications have error. They should be considered. Two examples of using this information are given.
Table 2. Measurement system components
|
Component |
Potential Error |
|
|
Balance |
Calibration |
|
|
Repeatability |
||
|
Linearity |
||
|
Hysteresis |
||
|
Corner loading error |
||
|
Rounding |
||
|
Drifting |
||
|
Standards |
Wrong class / out of tolerance |
|
|
Magnetic |
||
|
Different temperature |
||
|
Environment/installation |
Temperature |
|
|
Humidity |
||
|
Vibrations |
||
|
Drafts |
||
|
Operator |
Inadequate training |
|
|
Biased data selection |
||
|
Poor techniques |
||
|
Material weighed |
Hygroscopic / evaporates |
|
|
Electrostatic charge |
||
|
Magnetic |
||
|
Density difference |
||
|
Temperature |
||
Example 1: A Mettler Toledo publication, "Determining Weighing Uncertainty from Balance Specifications" provides a detailed method for using a balance’s error sources to estimate the uncertainty of its measurements.iv The author lists readability, repeatability, non-linearity, sensitivity, and temperature coefficient of sensitivity as potential errors. They correlate to the balance and environment components given in Table 3. Systematic errors due to the balance’s transfer characteristics are eliminated through adjustments after assembly or they are measured and stored in the balance so the can be compensated by signal processing algorithms. Design or calibration compensates for some sources of deviations. This method is derived from the probability theory that allows variances from uncorrelated sources to be added. The resulting sum may be considered the variance of all the influences considered.
Table 3. Uncertainty components of an AT 201 balance
|
Data sheet Specifications |
Value (SPC) |
Variance (SPC) |
||
|
Readability |
0.01 mg |
1x10-10 g2 |
||
|
Repeatability < 50 g |
0.015 mg |
2.3x10-10 g2 |
||
|
Repeatability 50-200 g |
0.04 mg |
1.6x10-9 g2 |
||
|
Non-Linearity w/in 10g |
0.03 mg |
9x10-10 g2 |
||
|
Non-Linearity w/in 200g |
0.12 mg |
1.4x10-8 g2 |
||
|
Sensitivity Accuracy |
1.5 ppm |
2.3x10-12 g2 |
||
|
Temperature Coefficient |
1.5 ppm/k |
2.3x10-12 g2 |
||
|
Environment (Assumption) |
Value (SPC) |
Variance (SPC) |
||
|
Ambient Temp. Excursion |
2°K |
4°K2 |
||
The paper has three sections:
Balance manufacturers cannot control the error effects that the balance operator; measurement process, environment and objects or material being weighed have on the total uncertainty of a measurement. Therefore, this method focuses on the balance’s error contributions on the uncertainty estimate and makes assumptions about the balance performance and some of the other sources of error. It is assumed that a balance performs within specifications, is operated according to good laboratory practices, and is used for determining small weights near capacity.
An example from the paper is paraphrased below. The assumptions minimize contributions from other components. These include making a small net weight near the capacity of balance so the repeatability specification for 200 g can be used. Also, no corrections are made for the degrees of freedom. An AT201 model balance is used with a 200g capacity and readability of 0.01 mg.
A sample of 1 g shall be weighed in a 190-g container. What is the resulting uncertainty of this weighing, conforming to a 95% confidence level? The formula valid for the combined normalized standard deviation for a single sample weighing is:
Srel = (1/m2 (SPCRP2
+ 2/3SPCNL2) + 1/3 (SPC CAL, rel2 1/3(SRCTCS*dt)2))^0.5
Srel = (1/(1g)2 (1.6x10-9
g2 + (2/3) 9x10-10 g2) + 1/3 (2.3x10-12)
+ 1/3(2.2x10-12*k-2*4k2))^0.5
Srel = (2.2x10-9 +1/3(2.3x10-12
+ 3.1x10-12)^0.5 = Srel = (2.2x10-9+
1.8x10-12)0.5= 47 x 10-6g
Conclusion: The mass of a 1 g sample, weighed in a 200g container, can be determined on this balance with a relative standard deviation of approximately 0.05 mg (Srel = 50x10-6 g). Based on a confidence level of 95%, the corresponding expanded uncertainty would be ~0.10 mg (Urel = 2* Srel = 1x10-4
These calculations were verified with the commercial software package "Uncertainty Analyzer" from the Integrated Sciences Group. Details about the software are available at http://www.isgmax.com. That program included degrees of freedom and produced a result that agreed within 5%. This software is useful for calculating uncertainty estimates using type B error or heuristic estimates in a manner that complies with the requirements of MU standards.
Example 2: Page 48 in the Sartorius publication gives the following example for calculating the uncertainty of measurement.v
Small amounts (approx. 5 g) are to be weighed on an analytical balance with a resolution of 0.1 mg. Ambient conditions are good (no incline, temperature difference of 5°C max; none of the containers or objects is electrostatically charged, nor is there any electromagnetic interference). The containers are small and must be correctly centered, as directed in the standard operating instructions.
With the exception of the reproducibility / standard deviation, all values are maximum errors. If the equation of u = 2 s is used to express the maximum uncertainty of the reproducibility and if the air buoyancy has been corrected, the uncertainty of the measurement will be as follows:
Table 4. Sartorius Example
|
Source of measurement uncertainty |
Standard Dev |
|
The reproducibility / standard deviation is: |
£ 0.1 mg |
|
The temperature coefficient for the sensitivity is £ 2.10-6, as stated in the technical specifications. Hence, the error for 5 g and ° D T = 5°C is £ 5 g * (2*10-6/C)* 5°C = |
£ 0.05 mg |
|
The maximum linearity error is as stated in the technical specifications: |
£ 0.2 mg |
|
The balance has been calibrated and adjusted with a standard E2 class weight of 200g (maximum error of 0.03 mg). In relation to a 5 g load is: |
£ 0.0075 mg |
|
The sample’s density is 2.0 g/cm3, with an uncertainty of 20%; the difference between the air buoyancy of the samples and the standard is thus 2.25 mg (systematic error). The uncertainty of this air buoyancy correction value due to a fluctuation in the density of 10% is: |
£ 0.225 mg |
|
And the uncertainty due to the assumed fluctuation in the sample’s density of 20% is: |
£ 0.45 mg |
U = Ö (2x 0.1mg) 2 +(0.05mg) 2 + (0.0075mg) 2 + (0.225mg) 2 (0.045) 2 = 0.58
However, if no correction is made for air buoyancy, a systematic error of 2.25 mg is add to the uncertainty of measurement "u" so that the total deviation can be as much as 2.83 mg.
These examples assume a worst-case scenario. The second example looks beyond the balance operation and the assumptions about the measurement process to point out a large systematic error in the direct weighing. In this case, the total uncertainty is more than 5 times the estimate derived from combining errors from the balance and material being weighed.
Method 2: Balance Calibration Data
The DKD document "Calibration of Non-automatic electronic Weighing Instruments"vi guideline document for DKD laboratories has several procedures for calibrating balances with single, multiple and adjustable ranges. With the collection of data from the linearity and corner loading tests, estimate of the temperature range and the temperature coefficient, the class of standards, operating range and magnitude of the object being weighed, an estimate of uncertainty can be determined. The guideline document is divided into a general part, a second part for single or multiple range balances with 1,000,000 or less scale divisions of 1 mg or larger, and a third part for single of multiple range balance with> 1,000,000 scale intervals and/or with scale intervals £ 0.01 mg.
Figure 2. Standards Laboratory Balance Calibration Report
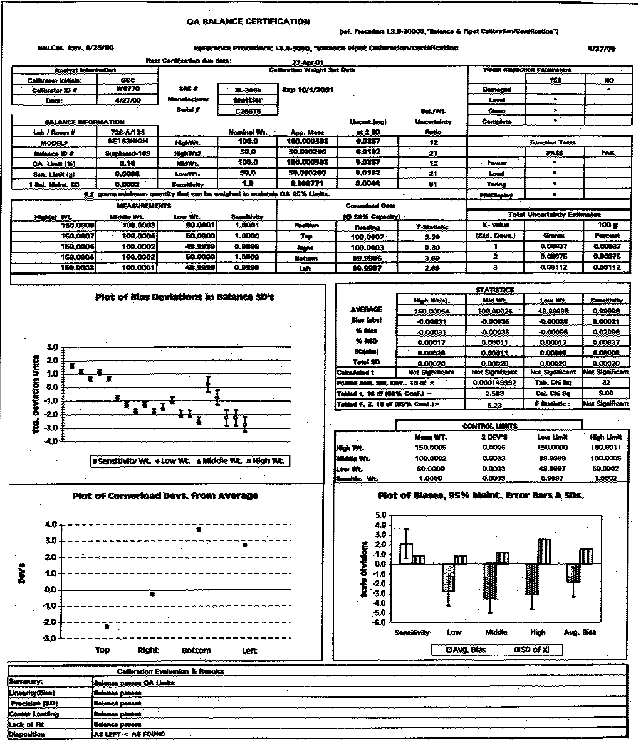
Several examples are provided in the reference. The procedure recommends the minimum number of weighings that should be taken for each error source and provides examples of the mathematical relationship between the scale reading and the various sources of error. The examples use data from balance calibrations that are plugged into the math models to calculate the MU based on empirical data take from a balance in it environment and under conditions the operator would encounter. These estimates capture more of the error sources than method 1 and verify the balance is performing within specified operating conditions.
At the SRS a spreadsheet-based calibration procedure is used. A copy of the balance calibration report is shown in Figure 2. The report satisfies the site QA requirements for calibration of M&TE. It includes standards used and their uncertainties and determines a ratio of the standard’s uncertainty at k = 1, to a maintenance limit, which is usually 2 scale divisions.
The calibration report includes graphs of the calibration measurement deviations and a summary of the observed bias and standard deviations observed at four points over the weighing range. An estimate of the balance uncertainty is given in the third group of numbers on the top right side of the report. The uncertainty estimate is given in scale divisions and as a relative percent of the mid –range reading. An estimate of the balance’s combined uncertainty is determined in a spread using the following equation:
U =SQRT ((MAX (U standard)/1000/2)^2+MAX (Pooled S or Maintenance S)^2+ABS (MAX (bias)/SQRT (6))^2+ABS (MAX (corner load value)/SQRT (6))^2).
This local balance calibration procedure has evolved over the past several years and attempts to provide as much useful data from the calibration effort as possible.
Method 3: Measurement Control Program Data
The first method estimates the MU for a target weight under given conditions using type B estimates of uncertainty from the manufacturer’s specifications and other sources. The method assumes the balance is operating within manufacturer’s specifications and the other sources of uncertainty contribute minimally to the observed weight reading on a balance. If the assumptions are correct, this is a reasonable estimate of MU. If the other components of the measurement process are not adequately controlled and or the balance is not functioning within manufacturer’s specifications, the MU estimate may be too small.
The second method is a combination of Type A and B estimates of MU from the balance and standards components. Experimental data are collected during the balance calibration over the operating range of the balance. If the balance performs outside of the manufacturer’ specifications, yet satisfies the customer’s measurement quality requirements, the calibration process provides objective data. This method captures the balance performance based on weighing standards. Calibrations are usually is performed by an outside organization. Therefore, the estimate does not include potential sources of error from the balance operator, material being weighed and variations in the environment, etc.
The third method uses measurement control program (MCP) data, which are based upon the reproducibility of the measurement system to demonstrate measurement performance within predefined control limits. The control program should duplicate the measurement process. In the example given below, two measurement processes are considered. The first is the standards laboratory’s mass calibration procedure. The second is a chemical laboratory’s gravimetric pipette calibration program.
The author described in detail how to determine "real time" estimates of MU in a paper presented at the "Weighing and Measurement in the Year 2000" international conference organized by the South Yorkshire Trading Standards Unit in 1997.vii
Commercially available software, JTIPMAPä, was evaluated in a demonstration program for the Department of Energy and reported in Westinghouse Savannah River Company document WSRC-MS-96-0032.viii Details about the software can be found at the http://www.jtipmap.com/index.htm web site. Some of the screen dumps from software are shown below as examples of how control charts are set-up and MC data are evaluated to maximize the information available in a MCP. This software, like any commercially available software has its strengths and weaknesses. The Savannah River Site (SRS) has several types of MCPs and uses commercial and custom developed software in the different laboratories. None are endorsed or recommended as a standard for this or any other DOE site. Many of the PMAP principles are applied in SRS MCPs.
Some of the screen dumps from JTIPMAPä software are shown below as examples of how control charts are set-up and the MC data are evaluated to maximize the information available in a MCP. This software, like any commercially available software has its strengths and weaknesses. The Savannah River Site (SRS) has several types of MCPs and uses commercial and custom developed software for various laboratories. None are endorsed or recommended as a standard for this or any other DOE site. Setting up a PMAP MCP involves selecting an artifact that represents the measurement process and calibrating it, if necessary, and then using it as a check standard to qualify a measurement system prior to using it to generate measurements for a customer. Once a PMAP is established, MC data are entered each time an operator uses a measurement system. The results of each check standard measurand are evaluated against up to three sets of control limits in the JTIPMAP. They are shown on Fig. 3. The computer based control charts are dynamic. They are updated with each additional data point and the current means of the control data are updated with each new result that is put into the computer. The charts are constructed to track data from two classes of operators. The first class is called the reference group. The metrologist or specialist who is well qualified usually generates this class of data. If production personnel, who are less skilled than, use the measurement system the specialists are, their data are entered as production data.
Figure 3. QC Chart of a Weight Calibration

The software is user friendly and prompts for basic information in setting up the initial PMAP control charts for a measurement procedure. Figure 4 shows the first of four cards from the pull down menu to be completed. The first card prompts for information on method and measurement, specifies the number of significant figures, and indicates the units. Check or control standard measurements can be expressed as the following: actual values, a ratio of measured to reference values, or a deviation from the reference value.

Fig. 5 shows card 2 which requires the following information for the control standard: the reference value (1 if normalizing control data), systematic uncertainty (drift for use and time) for the standard(s), and variability in the number of s used in the control charts (random error or precision), and documentation of the identity of a "check standard" that may be used off-line as an independent reference standard. The values obtained on the check standard may be tracked on a separate PMAP.
Card 3 in Fig. 6 contains information on 3 sets of limits and scaling information for the PMAP control chart. The limits include: reference limits are required (they are normally set by the best operators, who fully understand the effects of variables on the method performance); production limits are optional (all of the other operators make the production measurements under all lab conditions); and tolerance limits which represent the maximum permissible error that can be tolerated by the customer.
Fig. 7 shows Card 4 that is used for inputting optional information for the graphs of the control data. Each control chart will print up to 40 control measurements. Once this card is completed, all its information will be included on all charts. This information may include the metrologist in charge of the method and the person to be contacted if the method goes out of control. The method ID and related information should be included here, so it will provide all the information necessary on each and every control chart that is printed for hard copies that might be stored as permanent records.
Fig, 8 Shows the MU for the 1-Kg mass standard calibration values. It can be calculated at any time with all data collected since the last calibration of the measurement system. The random standard deviation of the check standard and the current set of data are squared, summed and the square root taken. Equations are shown below in the excerpt from the PMAP operating manual. This is an estimate of the standard uncertainty of the mass double substitution measurement system. It is multiplied by a coverage factor 2 that was specified on page three of the control chart set-up.
Fig. 8 shows the real time estimate of the potential uncertainty of calibrated kilogram mass standard is + 0.002060 and -0.001659 g under the conditions experienced in the Savannah River Standards Laboratory. These uncertainty values are asymmetric because they are the +/- 0.001863 g at k = 2 added to or subtracted from the observed mean systematic error or bias of 0.000204 g. Using the larger value would give an uncertainty estimate that contained both the bias and k times the standard uncertainty. These statistics are based on 58 measurements since the last calibration before 10/1/97.

The next example comes from repeated gravimetric calibrations of a 100 micro liter pipette. The weighing system captures the error sources from an analytical balance and the air buoyancy corrections under different environmental conditions.

Figures 9 and 10 are generated from a newer version of the software. In the new version an analysis of the calibration data provides an estimate of the process MU and the bias. The program is capable of tracking two variables and calculating the total uncertainty on each. The program lists one variable as the "reference" data and the other as "production line" data. The confidence level can be set at K = 1, 2, or 3. Figure 10 sets K = 3, so the MU is 0.9067 micro liters.

There are several advantages to using a MCP to capture the total variation of the measurement process. Many people do not what variables add uncertainty to their measurement process, so would underestimate the MU of their process. This method provides more of videotape of the measurement process, rather than the snap shot picture at time of calibration or from several assumptions.
A description of the uncertainty calculation is listed below from "Appendix C JTI PMAP Algorithms"
Calibrate
xi = each individual value under test (for i = 1 to n)
n = number of values under test
xbar = mean
s = JTIPMAP estimate of standard deviation
K = coverage factor
xbar = (å x i )/n
s = (å (x i - xbar
)^2/ (n - 1) ) ^ 1/2
+ K Sigma Limit = xbar + Ks Upper K standard deviation
limit
- K Sigma Limit = xbar - Ks Lower K standard deviation
limit
+/- 2K Sigma is expected to contain 95.4% of the values
if all test conditions are constant.
+/- 3K Sigma is expected to contain 99.7% of the values
if all test conditions are constant.
Process Measurement Uncertainty =
(xbar - Standard Value) +/- {K*(s2 + {Variability / K} 2)
^ 1/2 + ô Systematic Uncertaintyô
}
where:
xbar - Standard Value = JTI PMAP Systematic Error
Variability Sum = Variability portion of the Control
Standard uncertainty as
input of Setup Controls
Systematic Uncertainty = Systematic portion (bias or
drift for use/time) of the
Control Standard uncertainty as input on page 2 of Setup
Controls
The software performs many other useful functions; such as keeping a history file of the calibration data that can be used determine optimum calibration intervals. The software also includes statistical tests with built in critical values to test bias and s estimates of various calibration periods. This feature identifies significant changes that may be taking place in the control data, or between previous control periods.
After the uncertainty of the measurement system has been determined the user can use that estimate to make sure the right measurement instrument has been selected and that the right standards and methods are also selected to provide measurements that are fit for purpose.
Using process measurement assurance programs to estimate MU will capture the variation produced by the influence factors that make measurements uncertain. The first two methods provide estimates of uncertainty, but are more like snap shots versus a video of a measurement process. The third method provides a liberal estimate of MU that allows the measurement organization base their estimates on real data collected under actual operating conditions.
Summary
Knowledge of the quality of measurements is essential for managing processes. All measurements are estimates and have error that causes uncertainty about the true value. Quantifying the sources of uncertainty associated with a measurement involves determining an estimate of the MU. Three methods are commonly used for estimating the uncertainty of electronic balance measurements.
A major difference in the methods is the last method estimates the MU based on the reproducibility of the measurement system, not just balance sources of uncertainty considered and assumptions made that the influence factors are controlled or are negligible. The first two methods for estimating MU are based more on repeatability. The measurement organization needs to have MU estimates that will include all sources of variation that can make their measurements uncertain. The third method does this.
References