WSRC-MS-2000-00112
Predicting Stream Water Quality using Artificial Neural Networks
J. A. Bowers and C. B. Shedrow
Westinghouse Savannah
River Company
Aiken, South Carolina
This report was prepared as an account of work sponsored by an agency of the United States Government. Neither the United States Government nor any agency thereof, nor any of their employees, makes any warranty, express or implied, or assumes any legal liability or responsibility for the accuracy, completeness, or usefulness of any information, apparatus, product or process disclosed, or represents that its use would not infringe privately owned rights. Reference herein to any specific commercial product, process or service by trade name, trademark, manufacturer, or otherwise does not necessarily constitute or imply its endorsement, recommendation, or favoring by the United States Government or any agency thereof. The views and opinions of authors expressed herein do not necessarily state or reflect those of the United States Government or any agency thereof.
This report has been reproduced directly from the best available copy.
Available for sale to the public, in paper, from: U.S. Department of Commerce, National Technical Information Service, 5285 Port Royal Road, Springfield, VA 22161, phone: (800) 553-6847, fax: (703) 605-6900, email: orders@ntis.fedworld.gov online ordering: http://www.ntis.gov/support/ordering.htm
Available electronically at http://www.osti.gov/bridge/
Available for a processing fee to U.S. Department of Energy and its contractors, in paper, from: U.S. Department of Energy, Office of Scientific and Technical Information, P.O. Box 62, Oak Ridge, TN 37831-0062, phone: (865 ) 576-8401, fax: (865) 576-5728, email: reports@adonis.osti.gov
Abstract
Predicting point and nonpoint source runoff of dissolved and suspended materials into their receiving streams is important to protecting water quality and traditionally has been modeled using deterministic or statistical methods. The purpose of this study was to predict water quality in small streams using an Artificial Neural Network (ANN). The selected input variables were local precipitation, stream flow rates and turbidity for the initial prediction of suspended solids in the stream. A single hidden-layer feedforward neural network using backpropagation learning algorithms was developed with a detailed analysis of model design of those factors affecting successful implementation of the model. All features of a feedforward neural model were investigated including training set creation, number and layers of neurons, neural activation functions, and backpropagation algorithms. Least-squares regression was used to compare model predictions with test data sets. Most of the model configurations offered excellent predictive capabilities. Using either the logistic or the hyperbolic tangent neural activation function did not significantly affect predicted results. This was also true for the two learning algorithms tested, the Levenberg-Marquardt and Polak-Ribiere conjugate-gradient descent methods. The most important step during model development and training was the representative selection of data records for training of the model.
1 Introduction
The Savannah River Site (SRS), owned by the U.S. Department of Energy (DOE) is located on the upper Atlantic Coastal Plain of South Carolina, centered approximately 40 kilometers (25 miles) southeast of Augusta, Georgia. The entire location was declared a National Environmental Research Park in 1972 by the Atomic Energy Commission, the predecessor of DOE. Since its beginnings in the 1950s, the mission of the SRS was production of plutonium and tritium to support the defense, research, and medical programs of the United States government. The SRS mission currently is focused on national security work, recycling and reloading of tritium, environmental cleanup and legacy waste management. During this period, the focal points of environmental research and monitoring has shifted from thermal and other nuclear reactor-related effects to waste site characterization and restoration, bioremediation, innovative natural resource management, and National Environmental Policy Act (NEPA) support [1]. There are five main drainage basins on SRS. The five streams that originate on, or pass through SRS before entering the Savannah River, Upper Three Runs, Beaver Dam Creek, Fourmile Branch, Steel Creek, and Lower Three Runs. Environmental stewardship and environmental restoration efforts in these drainage basins necessitate the prediction of water quality variables in response to watershed inputs.
Although parametric statistical protocols and deterministic models have been the traditional approaches to forecasting water quality variables in streams, many recent efforts have shown that when explicit information of hydrological subprocesses are not needed Artificial Neural Networks (ANN) can be more efficient and effective [2,3]. Therefore, the purpose of this research was to apply our Site’s environmental monitoring data bases to ANN models to test their feasibility of predicting water quality parameters in SRS streams. Specifically, these tests would focus on efficiency of application in terms of time and therefore cost and ANN designs that prior efforts suggest would be effective for predictions.
2 Methods
2.1 Field methods
Mill Creek is a small tributary emptying into Tinker Creek which eventually drains into Upper Three Runs Creek system and further downstream into the Savannah River. The coniferous forest land cover type includes areas with predominately coniferous trees that are at least 6 m (20 ft) tall. Pines, primarily longleaf and loblolly pine, dominate the evergreen forested areas. Areas that have had recent logging and regeneration planting occupy a transitional land-cover type. These areas, classified as scrub-shrub, include areas of evergreen and deciduous shrubs and small trees 6 m (20 ft) or less in height with a canopy cover of at least 25%. Upland hardwood cover types include areas where the dominant species are deciduous trees at least 6 m (20 ft) tall. SRS soils range from seasonally wet and hydric to well-drained. Composition ranges from mostly sand-sized particles with high hydraulic conductivity rates to high clay content with moderately low to low hydraulic conductivity rates.
Water chemistry samples were collected from Mill Creek approximately 3.2 kilometers upstream of Mill Creek’s confluence with Tinker. The watershed encompassed by this station was 17.18 Km2 which is approximately 73% of the total Mill Creek watershed. During a 21-month period composite water samples were taken during both base and storm flow periods. During extended periods of little or no precipitation base flow conditions were established, while storm flow sampling was performed when storms seemed imminent. A peristaltic-pump sampler (ISCO 3700 Portable Sampler@) was used for 24–hour composite sample collections which consisted of 165 ml aliquots every 10 minutes for an hour filling a single sample container. Laboratory sample analyses followed United States Environmental Protection Agency (USEPA) protocols [4]. Daily mean precipitation records during the study period were obtained from the United States Geological Survey rain gauge database records located in the Mill Creek study area.
2.2 Data analysis and modeling methods
All of the data files were assembled into a HOPS@ data engine [5] and processed for loading into the neural modeling application MATLAB@ Neural Network Toolbox (Release 11) [6] running on a personal computer using the Windows@ NT4.0 operating system.
3 Results and Discussion
Our approach and execution were kept simple and conservative because of our inexperience with the methods and by recommendations in the peer-reviewed literature . Masters’ [7] very practical treatment of applying ANN methods to forecasting limited all ANN designs to the well-understood feedforward-backpropagation neural network. Additionally, the feedforward-backpropagation neural network has been shown to be an effective neural design for forecasting stream water quality variables [8,9,10,11]. All of the network designs used in this study consisted of one hidden layer with nonlinear activation functions (logistic or hyperbolic tangent) and a linear output layer.
The selection of variables reflected our long-term interest in applying neural networks to water quality and contaminant transport. Rainfall or precipitation rate obviously governs flows while, in turn, flow rates directly affect turbidity, total solids, total suspended solids and to a lesser degree total dissolved solids. Turbidity and total suspended solids are good parameters to monitor for soil erosion due to major construction runoff. Furthermore, particulate transport is directly proportional to those contaminants that are particle-bound [12].
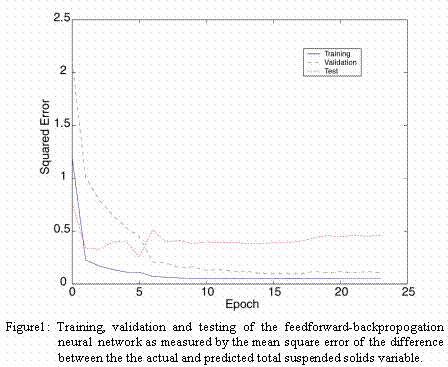
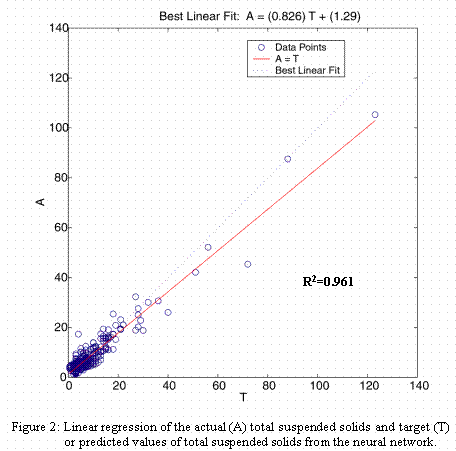
The first data set, 325 data records, was comprised of precipitation rate (mean inches per day), stream flow rate (mean cubic feet per second per day) and turbidity (turbidity units) with total suspended solids (mg/l) as the target output or predicted variable. The network model configuration set epoch number to 25, the Polak-Ribiere learning algorithm set to a learning rate of 0.1 and a logistic neural activation function. All variables were standardized by normalization of means and standard deviations. Training was governed by minimizing the mean square error between observed and predicted. Figure 1 illustrates the mean square error during training, validating and testing. One fourth of the total data was selected for training, one fourth for validation and the remaining one half for testing. Network performance was estimated by linear regression between the actual and target (predicted) total suspended solids after postprocessing the output to the original scalar variables (Figure 2).

After approximately 10 epoch cycles during training the network had reached a minimum mean squared error. Figure 2 indicates a satisfactory level of performance with an R value = 0.96. This level of agreement is very acceptable for a production application.
The model was again run using the hyperbolic tangent as the activation function with an almost insignificant difference with a linear regression giving an R = 0.95. Next the model was run altering only the learning algorithm using the Levenberg-Marquardt method. Again an insignificant difference with R = 0.95.
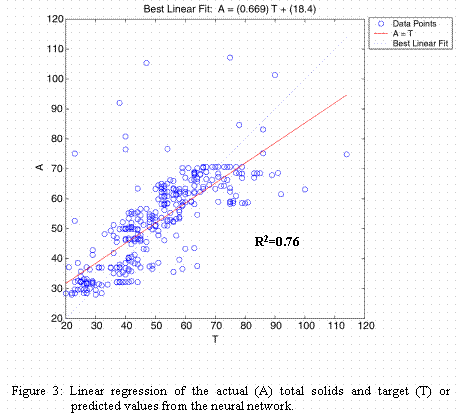
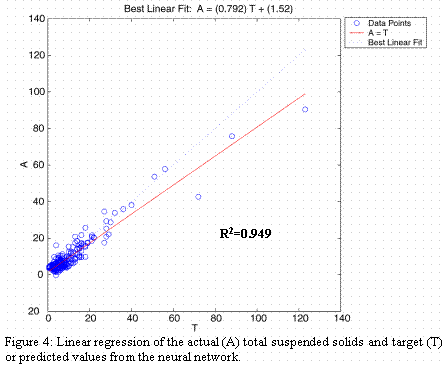
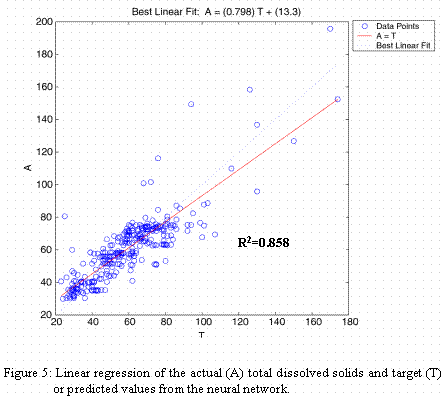
The second set of trials, again having 325 data records, was comprised of precipitation rate (mean inches per day), stream flow rate (mean cubic feet per second per day) and turbidity (turbidity units) with total solids (mg/l), total suspended solids (mg/l) and total dissolved solids (mg/l) as the predicted variables. Configuration of the neural model was exactly the same as in the first set of trials. These results were not as good as the first set of results. The training, validation and testing results are not shown. Figures 3, 4, and 5, present the regression results for total solids, total suspended solids and total dissolved solids, respectively. Although total suspended solids and total dissolved solids were predicted with reasonable results, total solids was not accurately modeled based on the data. A larger variation in total solids, seen in the raw data, could account for this result.
In the initial experiments presented here, the most significant impact on network ability to predict effectively is the partitioning of data into training, validation and testing, and making sure that the representativeness of data is optimized for training. Following literature guidelines, the inclusion of all of the domain of information, representing any subgroups in the information domain, and statistical representativeness [7] was not easily achieved. It is also important to note that the literature rarely addresses this important issue and should be a topic for further research. Subgroups in our data set followed weather patterns for the southeastern United States. Rainfall consisting of occasional heavy rain storms during the summer followed by weeks and sometimes nearly months of drought resulted in episodic spikes in precipitation and stream flow which cascaded through the water quality parameter responses. Our solution to representativeness in the data for training was to perform nested ascending sorts of the data to evenly distribute the data, and then select every fourth data record beginning with record number 1 for training. The validation set was comprised of every fourth record beginning with the third record. Selecting every fourth record, in sets of two beginning with the second and fourth record, constituted the test data set. This method proved to be the most effective and practical approach versus manually selecting data records based on distribution statistics which are very time consuming. However, planned future models having thousands or tens of thousands of data records with more input variables will require further development of techniques.
4 Conclusions
The application of a feedforward-backpropagation artificial neural network to the Mill Creek watershed data indicated its practicality to forecasting water quality variables at the Savannah River Site. As with any predictive modeling, data quality was paramount to effectiveness of predictions. When training data sets become large we recommend implementing a formal detailed analysis of the data for statistical representation. The feedforward-backpropogation neural model using a logistic activation function, a linear output function and the Polak-Ribiere learning algorithm proved a good design for the prediction of stream variables.
References